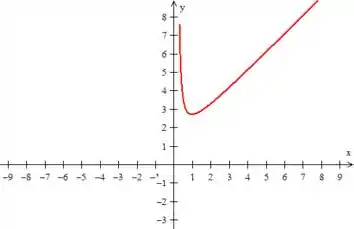
10. Esboce o gráfico da solução da equação do exercício anterior que satisfaz as condições iniciais:
Passo 1
No problema anterior, determinamos a solução geral da EDO que nos gerou o seguinte resultado:
Aplicando aquelas condições iniciais ali...
Aplicando segunda condição (mas antes derivando a solução)...
Aplicando agora...
Então, das duas equações...
Logo a resposta particular da nossa EDO será...
Passo 2
Desenhando ela em um gráfico, então teremos:
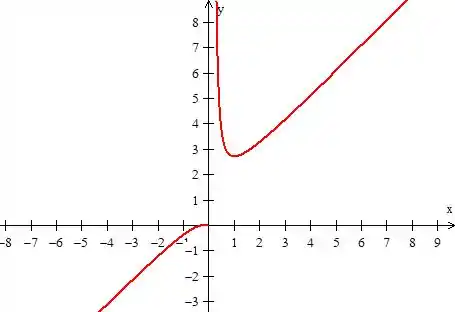
Mas assim. A condição de existência está atrelada a , então o gráfico não pode ter essa parte negativa:
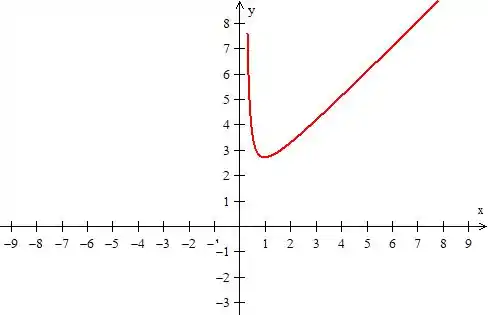
Resposta
E seu gráfico será: