16. Sejam e as temperaturas no instante , dos ambientes e , respectivamente. Admita que as temperaturas estejam variando nas seguintes taxas
Suponha que e .
A - Determine as temperaturas no instante , nos ambientes e .
B - Esboce os gráficos de , e , . Interprete.
C - Desenhe a temperatura descrita pelo ponto , .
Passo 1
Poxa! Determinar as temperaturas e no instante é resolver o sistema de EDO’s! Para fazer isso, primeiro devemos montar a matriz dos coeficientes:
E agora encontrar os seus autovalores !
Bem, como é apenas subtrair da diagonal principal...
Resolvendo o determinante...
Usando Báskara...
Ora, (o número imaginário) então...
A solução de um sistema de EDO com imaginário é:
Onde e são:
Ora, e vem do autovalor complexo:
No nosso caso:
Portanto...
Já e vem do autovetor complexo ( é a parte real e o imaginário). Vamos então determinar esse autovetor !
Passo 2
Os autovetores podem ser calculados assim:
Então para o teremos de coordenadas desconhecidas complexas :
Ora, sabemos que asta subtrair da diagonal:
Essas duas linhas são Linearmente dependentes e sempre serão! Então, basta pegar a primeira linha e multiplicar com a coluna e igualar a (produto de matrizes):
Se falarmos que , então...
Então um autovetor para é:
Lembre-se que você pode pegar outro valor para , desde que seja está valendo!
Aqui não precisa encontrar para o autovalor , pois só com o , já podemos falar quem é e quem é . Rescrevendo o vetor em parte real e imaginária...
Então...
Passo 3
Com isso podemos retornar para os valores de e ...
E substituir:
Então a solução será...
Juntando tudo vamos obter o seguinte...
Para determinar e , podemos usar o fato de que e :
Então...
E
Passo 4
O gráfico de em função do tempo é o gráfico de um cosseno:
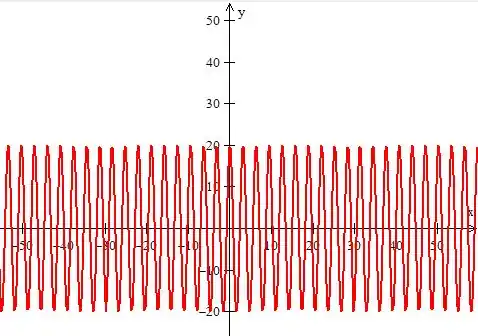
Só que com uma envoltória de , como no desenho:
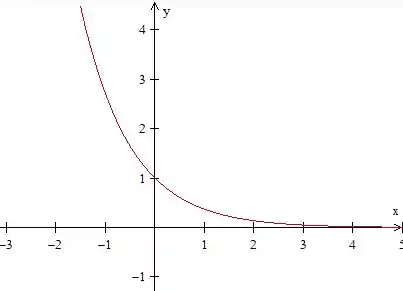
Então, o gráfico será assim:
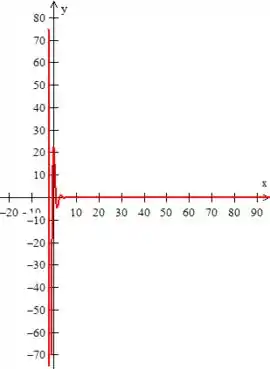
Já o gráfico de é bem parecido...
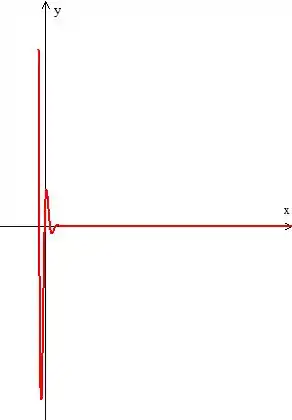
Veja que em ambos, a temperatura cai rapidamente a quando vai para o infinito.
Passo 5
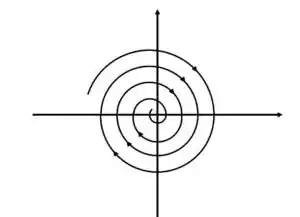
Ora, devido a exponencial negativa, as temperaturas tende a quando vaia para o infinito. O Retrato de fase então de um sistema de EDO de imaginário e com uma exponencial negativa é a espiral:
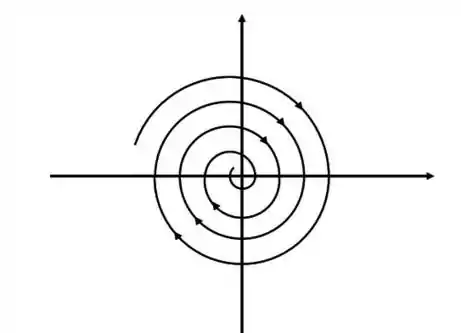
Resposta
Letra A:
Letra B: Gráfico de :
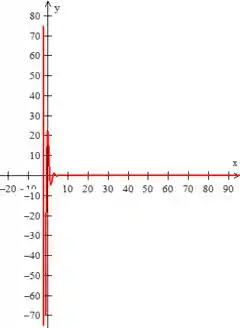
Gráfico de :
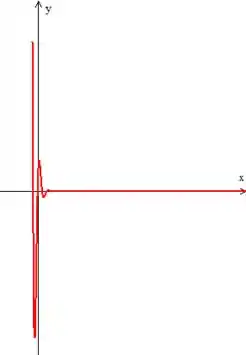
Letra C: