5. Para cada , seja Considere a função dada por
- Esboce os gráficos de e das
- , converge uniformemente a em E em com
Passo 1
Letra (a)
O domínio de é o conjunto de todos os para os quais a sequência converge. Sendo assim temos que proceder da seguinte forma:
Como temos uma indeterminação do tipo infinito sobre infinito, podemos aplicar L’H.
Logo,
O esboço do gráfico de é dado por:
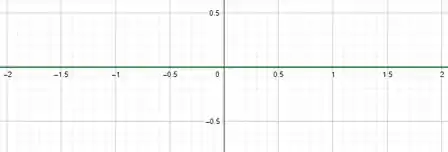
O esboço do gráfico de para um dos valores de n é dado por:
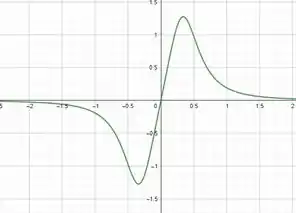
Passo 2
Letra (b)
Para convergência ser uniforme, dado tem que existir (que só depende de ) tal que
Para todo real. Como, para todo
Resulta que a convergência é uniforme em . E como o outro intervalo se encontra dentro do anterior, podemos que ela converge uniformemente no outro intervalor também.
Resposta
- Figura
- Demonstração