Calcule e interprete geometricamente o resultado obtido
Letra c)
Onde é a coroa circular
Com e é um real dado
Passo 1
O problema sugere uma integral de superfície e a superfície é a seguinte coroa circular
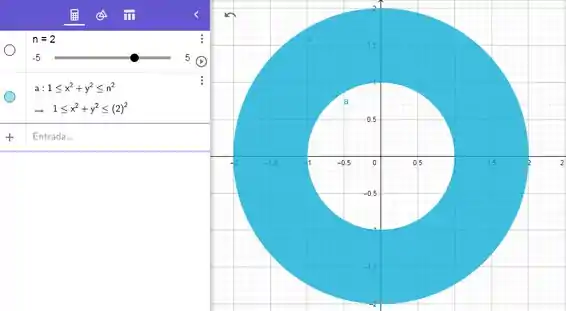
Passo 2
Se ao invés de resolvermos esta integral em coordenadas cartesianas, resolvermos em coordenadas polares o trabalho será deveras abreviado.
Podemos trabalhar em termos do ângulo teta () e dos raios () das circunferências que compõem a coros, ou seja, varia de até , ou seja varre todo o plano
O tamanho de é onde suas restrições podem ser obtidas
Para a restrição
tirando a raiz quadrada
E como agora estamos trabalhando com e os diferenciais não serão mais e sim
Passo 3
O resultado para será.
Logo o limite pode ser reescrito como
A primeira integral tem como resultado e a segunda
Então o limite ficará
Passo 4
Para
Igual a
Obtendo
Passo 5
Sendo
Pois a medida que aumenta o índice sobre fica cada vez mais negativo levando o limite a zero
Sendo
De forma análoga a medida que seja menor que 1 levará o índice sobre a valores positivos o que fará o limite assumir valor infinito
Resposta
Portanto
Se
Se