Considerando a sequencia com e para todo m, dada por:
Mostre que, em particular:
Interprete geometricamente
Passo 1
Bom galerinha, se nós analisarmos a letra (e) nós temos que:
Para o caso em que
Então, geometricamente, é a metade do lado de um polígono regular de lados circunscritos ao círculo de raio 1.
Se nós fizermos o nosso polígono terá 4 lados, na fórmula:
Se tirarmos do módulo:
Desenhando:
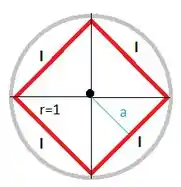
Quando nós calculamos a:
Neste caso nós temos que se multiplicarmos por quatro nós teremos o valor do semi-perímetro.
Passo 2
Se nós fizermos o nosso polígono terá 8 lados, na fórmula:
Se tirarmos do módulo:
O lado do octógono será igual a:
Neste caso o semi-perímetro é dado por:
Neste caso nós temos que se multiplicarmos por oito nós teremos um valor próximo ao do semi-perímetro do octógono.
A mesma informação nós podemos obter para os demais polígonos regulares !!
Tranquilinha, né?