8. Considere a equação
Uma função , , cujo gráfico tenha o aspecto abaixo, pode ser solução? Por quê?
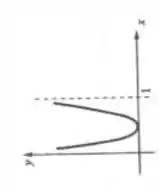
Passo 1
ÉEEEEEEE NÃO! Kkkkk
Não pode, pois no ponto mínimo dessa função, quase no meio de e , além de , a derivada da função também é zerada, justamente por ser um ponto mínimo:
POXA! De acordo com o teorema da Unicidade e existência, se uma função tem as mesmas condições iniciais, isto é:
Então podemos falar que ela é a mesma função solução da EDO:
Ora, qual é a função cuja derivada também é ? SIM! A função nula:
O que implicaria em...
Isso não é verdade, né? Na figura parece ser uma parábola e não a constante .
Resposta
Questão de demonstração.