Considere no plano um campo de forças conservativo , com energia potencial
isto é, . Uma partícula é abandonada na posição com velocidade nula. Seja
a posição da partícula no instante .
Prove que, para todo ,
Conclua que a partícula permanece na região , para todo . Que tipo de região é esta?
Passo 1
Essa é uma questão que vamos ter que lembrar um pouquinho de física:
O enunciado não disse isso, mas vamos supor que a massa da partícula é . Essa é a única forma de chegarmos no resultado pedido! Portanto,
Vamos tentar escrever as equações de movimento. Para isso, temos que achar :
Ou ainda,
Logo,
Vamos guardar essa duas equação equações!
Passo 2
Queremos mostrar que
Para isso, vamos chamar
Daqui a pouco você vai entender porque eu chamei esse termo de . Queremos mostrar que esse termo é igual a . Vamos provar primeiro que ele é constante. Para isso, basta tomar a derivada temporal:
Agora substituímos as equações do passo 1:
Fazendo isso:
Como a derivada é nula, temos que
Passo 3
Para calcular essa constante, basta usar a condição inicial:
Assim,
Portanto,
Demonstramos o que foi pedido!
Passo 4
Agora vamos a interpretação física do problema! Note que pode ser escrito como
O termo
é a energia cinética e é a energia potencial. A soma dos dois é a energia mecânica que é constate!
Passo 5
Note que podemos escrever:
Mas temos que
Logo,
Portanto,
Trata-se da região interna a uma elipse:
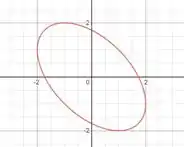
O movimento da partícula é restrito a essa região.
Resposta
Demonstração.