13. Considere o sistema
A - Determine condições para que
B - Determine condições para que a solução tenda para a origem quando , e em espiral.
Passo 1
Poxa! Aqui temos uma questão de Retrato de fase! Afinal, queremos que o ponto , vá para a origem em forma de espiral! Dessa forma aqui:
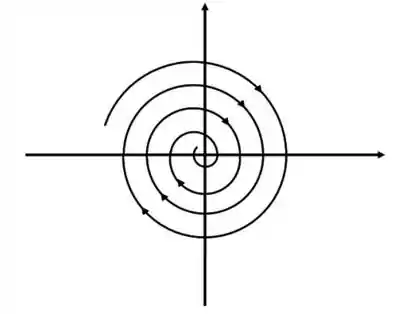
Para isso acontecer, a primeira condição é que ao resolver o sistema:
Devemos encontrar senos e cossenos. E isso só acontece quando???? ISSO MESMO! Quando temos autovalores complexos da matriz de coeficientes:
Passo 2
Ora, autovalores de matrizes podem ser encontrados assim:
Onde nada mais é que subtrair da diagonal principal::
Calculando o determinante então...
Observe que chegamos à uma equação do segundo grau para . Se resolvermos usando Báskara...
E a solução então...
Repare então que para termos autovalores complexos o deve ser negativo:
Além disso, é importante que seja negativo, pois só assim a espiral vai tender a , como vimos na letra A deste exercício.
Passo 3
Podemos ir um pouco mais profundo, pois sabemos que nada mais é do que:
Então...
Observe que esse termo do lado esquerdo, nada mais é do que o determinante da matriz dos coeficientes:
Então...
Essas então são as condições para ir em espiral: