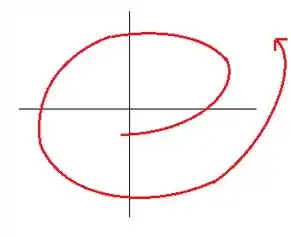
3 - Considere o sistema
Faça um esboço das trajetórias das soluções para suficientemente grande. Interprete.
Passo 1
Em sistema de soluções de EDO’s não homogênea, como sabemos temos que primeiro resolver a homogênea e depois a particular! O sistema homogêneo é:
Como já vimos de montão como resolver homogêneas, vou ser mais rápido aqui, beleza? A matriz de coeficientes é:
Então, os autovalores podem ser encontrados por:
Então...
Show! As soluções fundamentais então serão assim:
Quanto a e são os autovetores!
Passo 2
BUSCA PELOS AUTOVETORES: Vetor 1.
Os autovetores no caso são calculados assim:
Onde e são as coordenadas do nosso vetor . Como ...
Isolando em função de :
Escolhendo , então...
O autovetor então será:
BUSCA PELOS AUTOVETORES: Vetor 2.
Onde e são as coordenadas do nosso vetor . Como ...
Isolando em função de :
Escolhendo , então...
O autovetor então será:
Logo, as soluções fundamentais serão...
Ou, simplificando...
Passo 3
Com essas soluções fundamentais encontradas, podemos encontrar a solução da particular sabendo da formulinha marota:
Onde e são encontrados aqui
E o é o vetor que torna a coisa toda não homogênea:
Então vamos calcular essa integral aí!
Passo 4
Invertendo essa matriz:
Onde é o determinante da matriz original.
Então...
Logo...
Integrando então essa matriz integrando cada um dos termos:
Repare que não há necessidade de se colocar a constante de integração! A solução da particular então será:
Simplificando...
Passo 5
A solução geral então será:
ORA! Quanto estiver muito longe do , indo para o infinito mesmo, a exponencial maior vai prevalecer, isto é: . E a resposta vai ter uma cara assim:
Ou ainda, como não é nada perto de que está próximo ao infinito:
Então o desenho disso vai ser de uma espiral indo para o infinito:
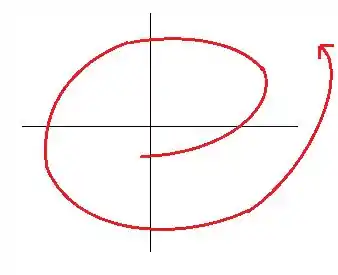
Resposta