Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.10 - Ex. 20

Determinar a área da região R delimitada pelas curvas y = x 3 , x + y = 2 e y = 0 .

Passo 1

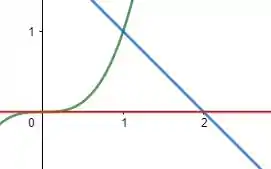
A área se dá pelo seguinte gráfico:

Passo 2

A equação da área se dá:

A = ∬ d A

Utilizando as informações obtidas, temos:

y 3 ≤ x ≤ 2 - y

0 ≤ y ≤ 1

Assim, a equação da área fica:

A = ∫ 0 1 ∫ y 3 2 - y d x d y

Passo 3

Integrando para x :

∫ y 3 2 - y d x = x

Aplicando os limites:

2 - y - y 3

Passo 4

Integrando para y :

∫ 0 1 ( 2 - y - y 3 )   d y = 2 y - y 2 2 - 3 4 y 4 3

Aplicando os limites:

1 - 0 ⋅ 2 - 1 - 0 ⋅ 1 2 - 1 - 0 ⋅ 3 4 = 2 - 1 2 - 3 4 = 3 4

Resposta

3 4   u . a .

Ver Outros Exercícios desse livro