Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.10 - Ex. 17
A integral iterada representa o volume de um sólido. Descrever o sólido.
Passo 1
Primeiramente, devemos analisar a integral dada e explicitar seus limites para cada eixo coordenado:
Passo 2
Agora, aplicaremos as limitações em um programa gráfico, obtendo assim o seguinte gráfico:
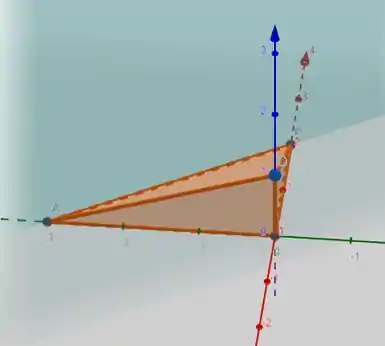
Desse modo, percebemos que a integral iterada representa o volume de um tetraedro
Resposta
Tetraedro.
Exercícios de Livros Relacionados
A integral iterada representa o volume de um sólido. Descrever o sólido. ∫ 0 4 ∫ - 2 2 4 - x 2 d x d y
Calcule o volume do conjunto dado. { x , y , z ∈ R 3 | 0 ≤ x ≤ 1 ,0 ≤ y ≤ 1 ,x 2 + y 2 ≤ z ≤ 2 }
Calcule o volume do conjunto dado. { x , y , z ∈ R 3 | 0 ≤ x ≤ 1 ,0 ≤ y ≤ 1 ,0 ≤ z ≤ x y e x 2 - y 2 }
Calcule o volume do conjunto dado. { x , y , z ∈ R 3 | 0 ≤ x ≤ 1 ,0 ≤ y ≤ 1 ,0 ≤ z ≤ x + 2 y }
Calcule o volume do conjunto dado. { x , y , z ∈ R 3 | 0 ≤ x ≤ 2 ,1 ≤ y ≤ 2 ,0 ≤ z ≤ x y }