Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.3 - Ex. 63
63. a) Determine se os limites a seguir existem e, em caso afirmativo, encontre-os.
b) Esboce os gráficos de no mesmo sistema de coordenadas e marque todos os pontos de intersecção.
c) Use um recurso gráfico computacional para gerar alguns membros da família e discuta o efeito da variação de e sobre a forma da curva.
Passo 1
a) Então galera, os limites que temos que calcular são:
Para o primeiro limite, temos:
Em outras palavras, não temos um resultado para esse limite, ou seja, ele não existe. Para o segundo limite, temos:
Como é uma função par, então:
Aplicando o limite, teremos:
Então esses são nossos limites, galera!
Passo 2
b) Esboçando o gráfico, teremos:
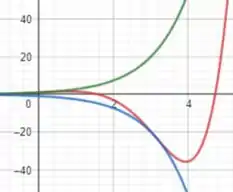
No qual a curva de azul é a função , a curva vermelha é a função e a curva verde é a função . Para encontrarmos os pontos de intersecção devemos igualar cada uma das funções para acharmos os respectivos valores de aonde as intersecções ocorrem, então bora lá!
Passo 3
Para e temos:
Isso nos dá:
No qual é qualquer valor natural, incluindo .
Para e temos:
Isso nos dá:
E esses são os pontos de intersecção!
Passo 4
c) Esboçar uma família de curvas da função que nos foi dada é adotar alguns valores de e para ver o comportamento da função. Logo:
Para e temos:
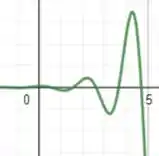
Para e temos:
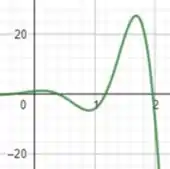
O que podemos notar nesses gráficos é que a frequência de oscilação se altera quando mudamos os valores de e , então essa é a implicação dessas constantes na curva!
Resposta
a)
b) e
c) e alteram a frequência de oscilação da curva.