Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.3 - Ex. 66
66. Seja , onde é a função dada no Exercício 65. Suponha que seja um ponto crítico de .
a) Estime .
b) Use o teste da derivada segunda para determinar se tem um máximo ou um mínimo relativo em .
Passo 1
a) Então pessoal, a função que nos foi dada é a seguinte:
E a função que o enunciado cita é dada através do gráfico de a seguir:
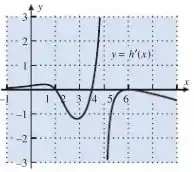
Se é um ponto crítico de , então temos que:
Derivando nossa função, teremos:
Passo 2
Se observarmos o gráfico que nos foi dado temos:
Ademais:
Substituindo na nossa expressão:
Passo 3
b) Derivando nossa derivada, teremos:
Simplificando:
Substituindo teremos:
Se observarmos o gráfico, notaremos que é negativa, pois a derivada primeira é totalmente negativa nesse intervalo. Sendo assim, pela multiplicação de sinais:
Se a derivada segunda nesse ponto é positiva, então a concavidade da função nas proximidades do ponto é para cima, o que indica um ponto de mínimo.
E esse é o nosso resultado, galera!
Resposta
a)
b)