Discuta como a reta tangente ao gráfico de uma função y = f x num ponto P x 0 , f x 0 é definida em termos de retas secantes ao gráfico pelo ponto P .

Enunciado

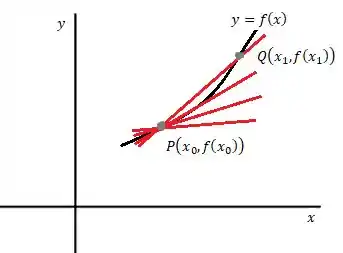
Vamos achar a reta secante de , ela une os pontos e visto no gráfico abaixo:

Ela é a reta com equação:

Agora temos que quando temos que e a equação da reta secante vai ser da forma:

Pronto, essa é a equação da reta tangente à curva no ponto .

Ei, a resposta está no passo a passo :)