Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.6 - Ex. 62
Use o Teorema do Confronto para mostrar que:
E ilustre o princípio envolvido usando um recurso gráfico computacional para fazer os gráficos de , e na mesma tela da janela .
Passo 1
Então galera, como sabemos que as funções trigonométricas variam de até , podemos escrever nosso teorema do confronto da seguinte forma:
Considerando que porque há um no denominador, temos que:
A partir disso, temos que quando o que acontece é que da mesma forma. Sendo assim, as desigualdades implicam que:
Que é exatamente o resultado que esperávamos e que o enunciado cede!
Passo 2
Para visualizarmos se, de fato, nosso resultado está correto, vamos plotar os gráficos de , e , se liga:
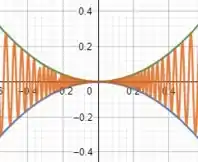
Por mais que esteja difícil de visualizar, temos que a função em verde (acima do eixo ) é , a função em azul (abaixo do eixo ) é e, por fim, a função em laranjado é . Pelo gráfico conseguimos notar que, de fato, o limite que encontramos está correto! E essa é a nossa análise da questão, pessoal!
Resposta
Ei, a resposta está no passo a passo :)