Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.6 - Ex. 64

Esboce os gráficos de , e , onde é uma função qualquer que satisfaz a desigualdade:

Para todo no intervalo . O que você pode dizer sobre o limite de quando ? Explique seu raciocínio.

Passo 1

Então galera, se esboçarmos os gráficos de , e , teremos o seguinte:

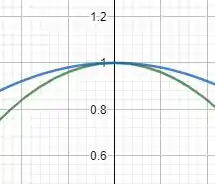
No qual a função em verde é e a função em azul é . Aqui vale ressaltar que a função é uma função que está entre essas duas funções, ou seja, no meio delas! Tudo bem, a primeira parte foi feita.

Passo 2

Para todo no intervalo temos que o limite de para se aproximando de zero será:

Oxe, mas por que esse é o resultado? Utilizando a noção do Teorema do Confronto, temos que as duas funções que estão “esmagando” a nossa estão se aproximando desse mesmo valor, então a consequência é que também se aproxima de para o intervalo dado! E essa é a nossa resposta, galera!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Prove que a equação x 3 - 4 x + 2 = 0 admite três raízes reais distintas.

Seja α a menor raiz positiva da equação x 3 - 4 x + 2 = 0 . Determine os intervalos de amplitudes 1 2 , 1 4 e 1 8 que contenham α .

Seja f contínua em a ,b e tal que fa fb . Suponha que quaisquer que sejam s e t em a ,b , s ≠t⇒fs ≠ ft . Prove que f é estritamente crescente em a ,b .(Observação: f estritamente crescente em a ,b⇔∀

Suponha que f : 0,1 → R seja contínua, f 0 = 1 e que f x é racional para todo x em 0,1 . Prove que f x = 1 para todo x em 0,1 .

Seja f : 0,1 → R contínua e tal que para todo x em 0,1 , 0 ≤ f x ≤ 1 . Prove que existe c em 0,1 tal que f c = c .