Encontre uma equação da parábola. A seguir, ache o foco e a diretriz.

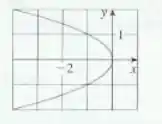
9.

Nessa questão, nos foi dado o gráfico de uma parábola para retirarmos dele sua equação, foco e diretriz. Pelo desenho, podemos concluir que , e é uma parábola no eixo , com concavidade para esquerda, o quer dizer que o sinal do é negativo.

Portanto, nossa parábola tem equação do tipo .

Agora para descobrir o valor de , vamos pegar um ponto do gráfico, por exemplo. Nesse ponto temos:

Então nossa equação procurada é