Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.5 - Ex. 31
Encontre uma equação para a cônica que satisfaz as condições dadas
31. Parábola, vértice , foco
Passo 1
Olá, meu amigo. Vou te ajudar a resolver essa atividade.
Nessa questão, nos foi dado o nome da cônica, seu vértice e foco para encontrarmos sua equação.
Bom, sabemos que é uma parábola, e parábolas tem equações no formato
A gente pode ver abaixo os gráficos genérico das parábolas centradas em
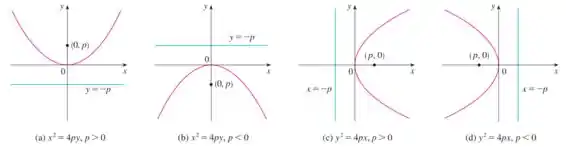
Como temos , sabemos que essa é uma parábola com eixo no eixo , portanto da forma
Também sabemos que o foco de uma parábola pode ser encontrado por , então temos .
Agora é só a gente substituir o que faltava na equação geral.
Passo 2
E como o vértice é , não temos nenhum número somando ou subtraindo de e assim, nossa equação fica:
Resposta
Exercícios de Livros Relacionados
Desenhe um esboço do gráfico da equação: x * y = - 2
Desenhe um esboço do gráfico da equação: x^2 * y^2 = 4
Ache uma equação da circunferência satisfazendo as condições dadas: O centro está em - 2 ,5 e é tangente à reta x = 7 .
Ache uma equação da circunferência satisfazendo as condições dadas: O centro está em - 3 , - 5 e é tangente à reta 12 ⋅ x + 5 ⋅ y = 4 .
Ache uma equação da reta que é tangente à circunferência x 2 + y 2 - 4 ⋅ x + 6 ⋅ y - 12 = 0 no ponto 5 ,1 .