Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.7 - Ex. 59

Encontre equações polares para os círculos nos Exercícios 57-64. Esboce cada círculo no plano coordenado e classifique-o com suas equações cartesianas e polares.

x 2 + ( y - 5 ) 2 = 25

Passo 1

Salve, fera! Tudo bem? Essa questão pode não ser tão simples. Vamos encará-la juntos?

Neste problema, nosso objetivo usar as relações a seguir para transformar os círculos de coordenadas cartesianas para coordenadas polares.

r 2 = x 2 + y 2 ,   x = r cos ⁡ θ     e     y = r sen ⁡ θ

Em seguida, iremos esboçar o gráfico. E fim de papo.

Simbora?

Passo 2

Vamos começar desenvolvendo o produto notável da nossa equação cartesiana:

x 2 + y 2 - 10 y + 25 = 25

x 2 + y 2 - 10 y = 0

x 2 + y 2 = 10 y

Usando as relações dadas no passo 1, obtemos:

r 2 = 10 r sen ⁡ θ

Dividindo ambos os lados por r, conseguimos nossa equação polar da circunferência:

r = 10 s en ⁡ θ

Passo 3

Pela equação inicial e sabendo a equação geral de uma circunferência é dada por:

x - x c 2 + y - y c 2 = r 2

Temos que seu raio é r = 5 e o centro tem coordenadas ( 0 , 5 ) .

E o seu gráfico terá o seguinte formato:

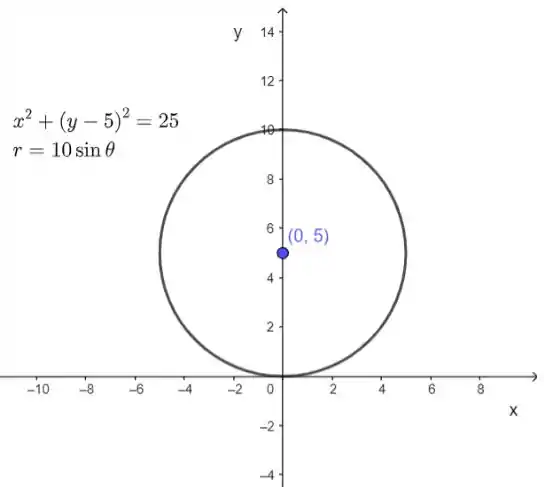
Espero ter ajudado! Abraços e até a próxima!

Resposta

r = 10 sen ⁡ θ .

Exercícios de Livros Relacionados

Nos exercicos de 37 a 52, ache os pontos de intersecção dos gráficos do par de equações dadas. Faça um esboço de cada par de gráfico com o mesmo eixo polar e a mesma origem. r = sen ⁡ θ r =sen ⁡ 2 θ
Nos exercicos de 37 a 52, ache os pontos de intersecção dos gráficos do par de equações dadas. Faça um esboço de cada par de gráfico com o mesmo eixo polar e a mesma origem. r sen ⁡ θ = 4 r cos ⁡ θ =
Nos exercicos de 37 a 52, ache os pontos de intersecção dos gráficos do par de equações dadas. Faça um esboço de cada par de gráfico com o mesmo eixo polar e a mesma origem. r ² sen ⁡ 2 θ = 8 r cos ⁡
Nos exercicos de 37 a 52, ache os pontos de intersecção dos gráficos do par de equações dadas. Faça um esboço de cada par de gráfico com o mesmo eixo polar e a mesma origem. r = t gθ r = 4sen ⁡ θ
Nos exercicos de 37 a 52, ache os pontos de intersecção dos gráficos do par de equações dadas. Faça um esboço de cada par de gráfico com o mesmo eixo polar e a mesma origem. r = 2 cos ⁡ 2 θ r = 2sen ⁡