Esboce o desenho do sólido descrito pelas desigualdades
Passo 1
Para desenhar o gráfico deste sólido podemos verificar quanto vale para o plano cartesiano.
Sabemos que , então:
Podemos verificar então que corresponde a um paraboloide circular que começa em e vai até , isso pois:
Sendo o limite da primeira curva da ineuqação.
Em seguida começa a segunda curva:
que vai até o ponto .
Passo 2
Desta forma o gráfico do sólido é:
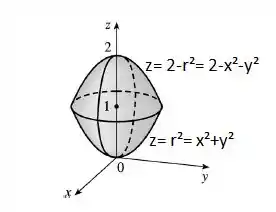
Resposta
Ei, a resposta está no passo a passo :)