Utilize um dispositivo gráfico para desenhar o sólido envolvido pelos paraboloides e .
Passo 1
Para facilitar o desenho do gráfico vamos passar os paraboloides para coordenadas cilíndricas.
Para isso vamos utilizar que:
Desta forma temos:
E
Como queremos o sólido que envolve os dois paraboloides vamos igualar as equações:
Então o sólido que queremos plotar o gráfico é dado pela seguinte inequação em coordenadas cilíndricas:
Passo 2
Desta forma o gráfico é:
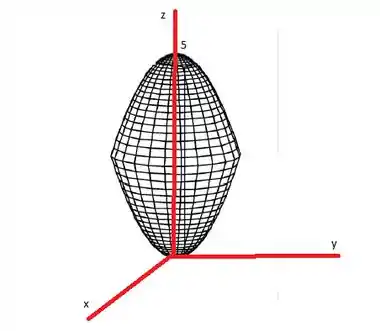
Resposta
Ei, a resposta está no passo a passo :)