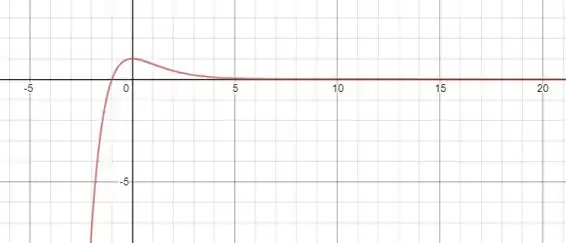
Esboce o gráfico da solução que satisfaz as condições iniciais dada.
Passo 1
O exercício pede para reolver a EDO homogênea de segunda ordem
Como os coeficientes são constantes, caímos na equação característica
As soluções dessa equação são
Quando as raízes são duplas, temos que
Portanto, com :
Passo 2
Como , temos que
Portanto,
Logo,
Como :
Portanto,
Um esboço do gráfico é dado a seguir: