Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 22
Esboce a região delimitada pelas curvas indicadas e encontre sua área.
Passo 1
De inicio, vamos representar o gráfico. Para , temos uma reta passando pela origem.
Então, o nosso gráfico fica assim:
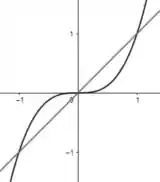
Fazendo a interseção das equações temos:
Esse será o nosso intervalo de integração. Agora podemos calcular a área!!
Passo 2
Essa integral pode ser dividida em duas partes pois os intervalos de integração são iguais, logo
Então,
Resposta
Exercícios de Livros Relacionados
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da