Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 18
Esboce a região delimitada pelas curvas indicadas e encontre sua área.
Passo 1
Opa, bora resolver esse problema! O enunciado nos dá as curvas:
Temos uma função raiz com a raiz e uma reta, que podemos colocar em evidência:
Podemos calcular quando a reta intercepta e :
Além disso podemos calcular o ponto onde a curva e a reta se interceptam:
Elevando os dois lados ao quadrado:
Qando temos que:
Então as curvas também vão se interceptar nesse ponto! Agora podemos esboçar o gráfico:
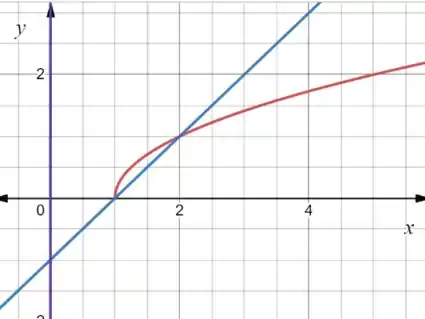
Onde a curva azul é e a curva vermelha é .
Passo 2
Agora vamos montar a integral! A área que vamos calcular vai ser dada pela subtração entre a curva vermelha e a curva azul e os limites de integração serão os pontos de intersecção que calculamos! Temos então:
A primeira integral a gente pode resolver por substituição, fazendo:
Agora a segunda parte:
Juntando e aplicando os intervalos de integração:
Então:
Prontinho!