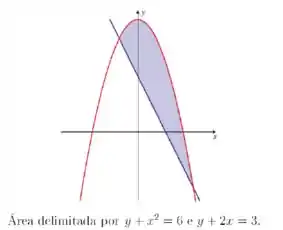
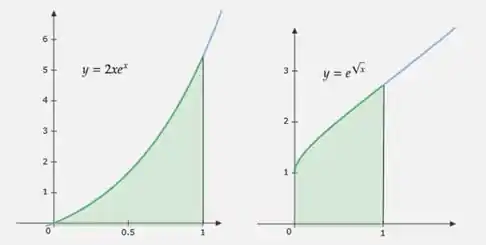
Exercícios de Área entre Curvas - Lista de Exercícios Resolvida
Questão 2
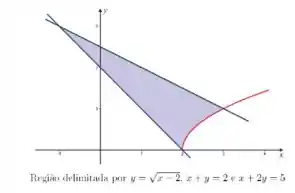
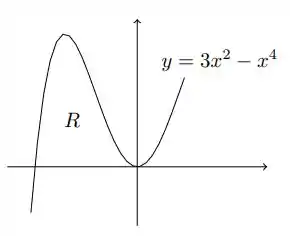
Considere a região delimitada pelas curvas e
Esboce a região .
Calcule a área da região .
Ver solução completaQuestão 3
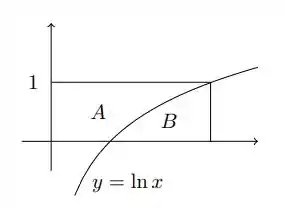
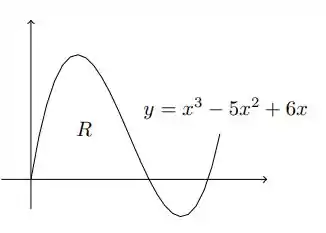
Calcule a área da região compreendida entre o gráfico de
E o eixo , com
Ver solução completaQuestão 4
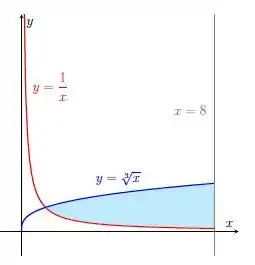
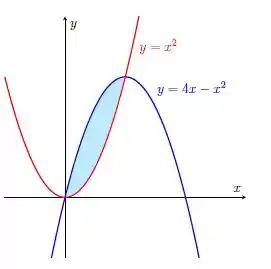
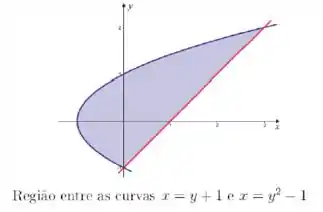
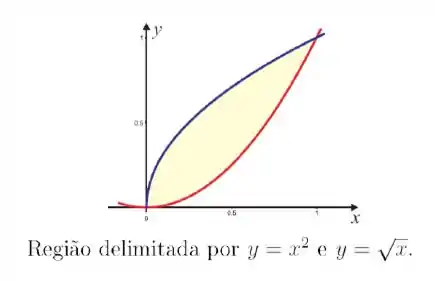
Calcule a área da região limitada pelas curvas e . Faça um esboço da região.
Ver solução completaQuestão 5
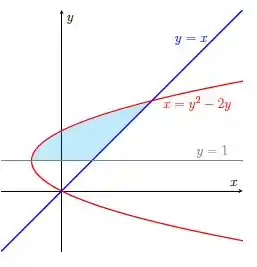
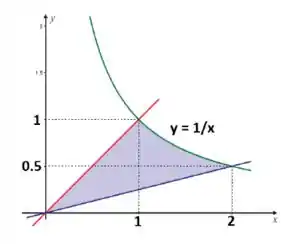
Seja a região limitada entre e o eixo . Encontre a equação da reta que passa pela origem e que divide em duas subregiões com áreas iguais.
Ver solução completaQuestão 7
Determine a área da região , onde:
é a região limitada pela curva , pelo eixo e pelas retas e .
Ver solução completaQuestão 9
Esboce a região correspondente a cada uma das integrais definidas, depois calcule as integrais.
a)
Ver solução completaQuestão 11
Esboce a região do plano delimitada pelos gráficos e e calcule sua área.
Ver solução completaQuestão 12
Calcule a integral
onde é o pedaço dada curva dada pela equação , com , , orientada no sentido anti-horário. Justifique.
Ver solução completaQuestão 13
Dado o gráfico de abaixo, determine a área compreendida entre os gráficos de e , para .
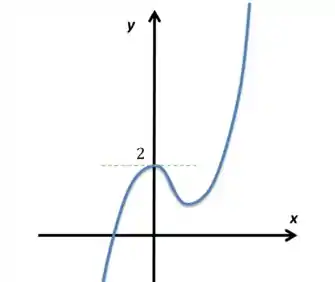
Questão 14
Determine a área da figura plana delimitada pelos gráficos de e e pelas retas e .
Ver solução completaQuestão 15
Calcule a área da região limitada compreendida entre os gráficos de e .
Ver solução completaQuestão 17
Na figura abaixo, sabendo que , a reta é a reta horizontal e a reta é tangente ao gráfico da em , ache a área da região cinza.
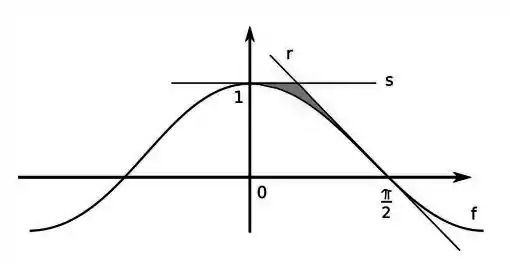
Questão 18
Considere os pontos e
- Determine a equação da reta que passa por estes dois pontos
- Determine a equação da parábola que também passa por estes dois pontos.
- Determine a área da região delimitada pela reta e pela parábola acima.
Questão 19
Considere a região delimitada pela parábola , pela reta tangente a esta parábola em e pelas retas e .
Esboce a região , indicando claramente a região na sua figura.
Determine a equação da reta tangente à parábola em .
Encontre a área da região
Ver solução completaQuestão 24
Os gráficos de
Se interceptam quatro vezes, limitando duas regiões. Encontre a área dessas regiões.
Ver solução completaQuestão 26
Considere as funções e . Calcule a área da região limitada pelos gráficos de e no intervalo .
Ver solução completaQuestão 27
Seja a região limitada entre e o eixo . Encontre a equação da reta que passa pela origem e que divide em duas subregiões com áreas iguais.
Ver solução completaQuestão 28
Calcule a área da região entre os gráficos das funções e e as retas e
Ver solução completaQuestão 29
Calcule a área da região indicada na figura abaixo, onde corresponde a reta e :
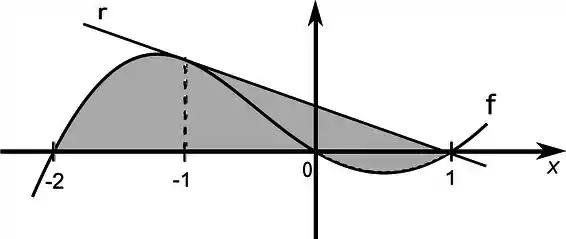
Questão 30
5) Seja a região localizada no primeiro quadrante do plano cartesiano, cujos pontos estão localizados acima da reta , abaixo da parábola e abaixo da hipérbole .
- Esboce , indicando os pontos de interseção das curvas
- Calcule a área de
Questão 34
3) Considere a região plana
- Esboce a região
- Escreva a área de como uma integral na variável
- Calcule a área da região utilizando o método que preferir
Questão 37
Esboce a região delimitada pelas curvas e decida se a integração deve ser feito com relação a variável x ou y. Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área de integração.
I)e
Ver solução completaQuestão 39
Calcule a área da região interior à lemniscata e exterior à circunferência de centro na origem e raio unitário.
Ver solução completaQuestão 42
Esboce e encontre a área da região delimitada pelo gráfico de , pela reta e pelos eixos e .
Ver solução completaQuestão 44
Calcule a área da região limitada pela curva de equação e por sua assíntota, situada À direita do eixo .
Ver solução completaQuestão 45
Esboce as regiões do plano delimitadas pelos gráficos e e calcule a área de cada uma dessas regiões.
Ver solução completaQuestão 48
Sejam b um número real positivo e R a região do primeiro quadrante do plano cartesiano situada abaixo dos gráficos de e . Seja S o sólido obtido pela rotação de R em torno do eixo x, cujo volume é igual a V. Sabe-se que V = . Calcule o valor de .
Ver solução completaQuestão 51
Considere a região do primeiro quadrante limitada pelas curvas , e .
- Esboce a região .
- Calcule a área de .
Questão 54
Esboce a região delimitada pelas curvas e e calcule o valor numérico de sua área.
Ver solução completaQuestão 56
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região
(11) ,
Ver solução completaQuestão 59
Seja a região do primeiro quadrante limitada pelos eixos coordenados e por . Suponha que a reta divida em duas sub-regiões de mesma área. Então vale:
Questão 63
2) Seja a região plana delimitada pelas curvas , e conforme o esboço abaixo:
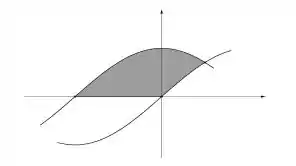
- Escreva a área da região através de uma soma de integrais.
- Calcule a área da região .
Questão 64
Questão 1:
Sejam e funções dadas por
e
e considere a região dada por
- Esboce a região .
- Escreva a área da região como uma soma de duas integrais na variável .
- Escreva a área da região como uma soma de duas integrais na variável .
- Calcule a área da região .
Questão 65
Questão 4: Sabe-se que as curvas e intersectam-se em exatamente três pontos com abscissas , e , respectivamente, onde é um número real negativo.
Calcule a área total, em termos de , da região entre as curvas para .
Dica: Faça um esboço destacando os pontos importantes e lembre-se que .
Ver solução completaQuestão 66
Questão 4) Considere as funções e . Calcule a área da região limitada pelos gráficos de e no intervalo .
Ver solução completaQuestão 67
Considere a função dada por:
(a) Esboce o gráfico de
(b) Considere a região definida por:
Escreva a área de como uma soma de integrais na variável
Ver solução completaQuestão 69
Considere a função dada por
- Determine os intervalos de crescimento e decrescimento de
- Determine os intervalos onde o gráfico de tem concavidade voltada para cima e onde tem concavidade voltada para baixo.
- Faça um esboço do gráfico de indicando explicitamente as abscissas dos pontos de máximo, de mínimo e de inflexão.
- Sejam e as duas raízes da função no intervalo , , calcule
Questão 71
Q04) Seja a região compreendida entre os gráficos das funções , e . Faça o que se pede abaixo:
- Esboce a região , explicitando quais são os pontos de interseção entre as curvas.
- Escreva (mas não calcule!) integrais que representem a área de .
Questão 72
4) Considere a região do plano limitada pelas curvas e com
- Faça um esboço das curvas envolvidas no problema, indicando os pontos notáveis e hachurando a região .
- Calcule a área da região .
Questão 73
Desenhe o conjunto abaixo e calcule a área:
f) é a região do plano compreendida entre o eixo e o gráfico de , com .
Ver solução completaQuestão 76
Encontre a área da região sob a curva , no intervalo . Interprete geometricamente o resultado.
Ver solução completaQuestão 77
Seja . Considere a função definida por:
(a) Determine o valor de para que a função seja contínua e diferenciável em
(b) Seja o valor determinado no item anterior.
(b.1) Calcule
(b.2) Seja a região limitada pelo gráfico de e o eixo . Calcule a área de
(b.3) Os resultados dos itens (b.1) e (b.2) deveriam ser iguais? Justifique sua resposta
Ver solução completaQuestão 78
- Determine os valores de para os quais
- Sejam e os valores encontrados no item , determine a equação da parábola que tem vértice em e cujos pontos de interseção com o eixo são e
- Esboce a região abaixo onde é a função determinada no item e e são os valores encontrados no item
- Calcule a área da região
Ver solução completaQuestão 81
1.3 Seja a região finita do plano, delimitada pelas curvas e . A área dessa região é representada pela expressão integral:
Questão 82
2) Esboce a região delimitada pelas curvas e decida se a integração deve ser feita com relação a variável ou . Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área da região.
b)
Ver solução completaQuestão 83
Considere dada por , e a reta tangente a seu gráfico no ponto de abscissa 4. Se é interceptado desta reta com o eixo , então a área hachurada na figura (fora de escala) abaixo é:
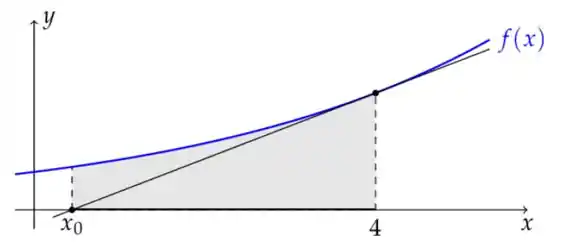
Questão 85
2. Calcule a área da região do primeiro quadrante limitada pelo eixo dos , pela reta e pela curva . Faça um esboço da região, identificando claramente todos os pontos de interseção.
Ver solução completaQuestão 86
Considere a função
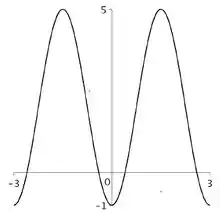
- Sabendo que a curva acima é o gráfico de , determine
- Determine todos os valores de que satisfazem a equação
- Calcule a área da região
Questão 87
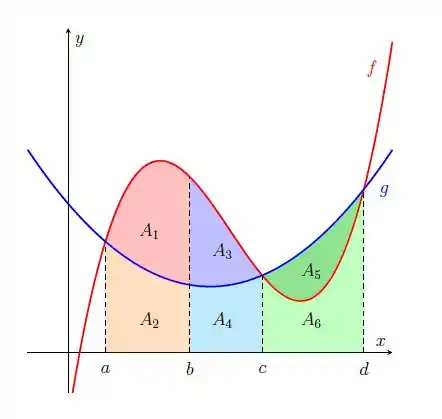
- Escreva o resultado das integrais em termos das medidas das áreas
Questão 90
Em cada item, determine a área da região delimitada pelos gráficos das curvas.
b) , , e .
Ver solução completaQuestão 91
Em cada item, determine a área da região delimitada pelos gráficos das curvas.
c) , , e .
Ver solução completaQuestão 92
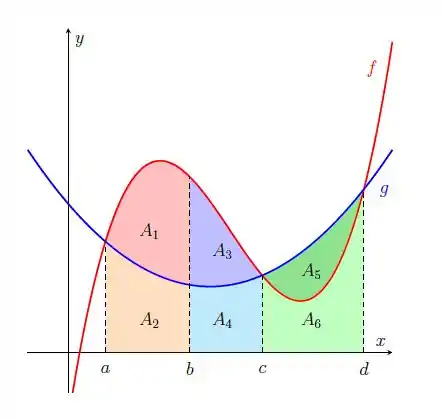
- Escreva as áreas e em termos de integrais
Questão 93
Em cada item, determine a área da região delimitada pelos gráficos das curvas.
a) , , e .
Ver solução completaQuestão 94
Em cada item, determine a área da região delimitada pelos gráficos das curvas.
d) , , e .
Ver solução completaQuestão 95
Em cada item, determine a área da região delimitada pelos gráficos das curvas.
f) e .
Ver solução completaQuestão 96
Em cada item, determine a área da região delimitada pelos gráficos das curvas.
g) e .
Ver solução completaQuestão 97
Em cada item, determine a área da região delimitada pelos gráficos das curvas.
i) , e
Ver solução completaQuestão 98
Em cada item, determine a área da região delimitada pelos gráficos das curvas.
h) e
Ver solução completaQuestão 100
Considere a região do plano limitada pelas curvas e , com
Esboce a região , destacando os pontos notáveis da mesma.
(Atenção: não precisa determinar detalhadamente o crescimento/decrescimento nem a concavidade das funções envolvidas.)
Calcule a área de
Ver solução completaQuestão 102
2) Esboce a região delimitada pelas curvas e decida se a integração deve ser feita com relação a variável ou . Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área da região.
f)
Ver solução completaQuestão 103
Ache a região delimitada pela parábola a reta tangente a está parábola no ponto (1,1) e o eixo x
Ver solução completaQuestão 104
O gráfico abaixo representa a velocidade de um carro em função do tempo. Esboce o gráfico da posição do carro em função do tempo.
Ver solução completaQuestão 105
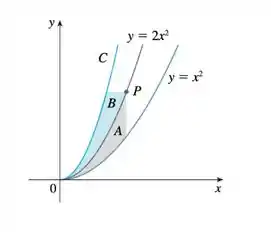
A seguinte figura mostra uma curva C com a seguinte propriedade: para cada ponto P na curva , as áreas e são iguais, ache uma equação para C.
Questão 107
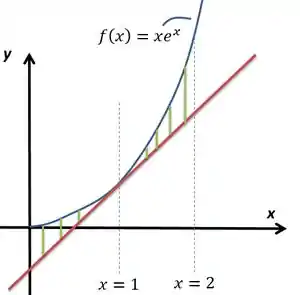
Considere definida por e a reta tangente ao gráfico da em . Calcule a área da região destacada na figura abaixo:
Questão 110
Seja a região limitada do plano que é delimitada pelas curvas:
Sabendo que o gráfico da função , com , divide em duas regiões de área iguais, o valor de é
a)
b)
c)
d)
e)
Ver solução completaQuestão 111
Calcule a área da parte do paraboloide que está abaixo do plano (adaptado)
Ver solução completaQuestão 112
Suponha que 2J de trabalho sejam necessários para esticar uma mola de seu comprimento natural de 30 cm para 42 cm.
a) Encontre a função de força f(x).
b) Quanto trabalho é necessário para esticar a mola de 35 cm para 40 cm?
Ver solução completaQuestão 114
Encontre a área da região limitada pelo gráfico das funções e para .
Ver solução completaQuestão 115
Encontre a área da região limitada acima por , abaixo por e nas laterais por e .
Ver solução completaQuestão 119
Questão 4. Seja a superfície dada pela parte da esfera , calota esférica, que está acima do plano . Considere a função definida em uma região de que contém .
(c) Calcule a área da superfície .
Ver solução completaQuestão 120
Considere a área da região de intersecção às curvas e . Esboce a região
Parte II) Calcule a área da região de intersecção
Ver solução completaQuestão 121
Considere a região plana limitada pela curva , pelo eixo e pelas retas e .
Calcule a área de por uma ou mais integrais definidas em termos de .
Ver solução completaQuestão 122
Considere a região plana limitada pela curva , pelo eixo e pelas retas e .
Use o item anterior para obter por meio das áreas ali calculadas.
Ver solução completaQuestão 123
Considere a região compreendida entre os gráficos de e , sabendo que os vértices da região considerada ocorrem em e .
Encontre a área da região .
Ver solução completaQuestão 124
Desenhe o conjunto abaixo e calcule a área:
p) é o conjunto de todos os pontos tais que e .
Ver solução completaQuestão 125
Determine a área da região limitada pelo gráfico da função e o eixo com .
Ver solução completaQuestão 126
Desenhe o conjunto abaixo e calcule a área:
n) é o conjunto de todos os pontos tais que .
Ver solução completaQuestão 127
Desenhe o conjunto abaixo e calcule a área:
j) é o conjunto de todos tais que e .
Ver solução completaQuestão 128
Desenhe o conjunto abaixo e calcule a área:
k) é o conjunto do plano limitado pela reta , pelo gráfico de com .
Ver solução completaQuestão 129
Desenhe o conjunto abaixo e calcule a área:
g) é o conjunto do plano limitado pela reta e pelo gráfico de , com .
Ver solução completaQuestão 130
Desenhe o conjunto abaixo e calcule a área:
h) é o conjunto do plano limitado pelas retas , , e pelo gráfico de .
Ver solução completaQuestão 131
Desenhe o conjunto abaixo e calcule a área:
i) é o conjunto do plano limitado pelas retas , , e pelo gráfico de .
Ver solução completaQuestão 133
Desenhe o conjunto abaixo e calcule a área:
o) é o conjunto de todos os pontos tais que .
Ver solução completaQuestão 134
Desenhe o conjunto abaixo e calcule a área:
m) é o conjunto do plano limitado pelas retas , e pelos gráficos de e .
Ver solução completaQuestão 135
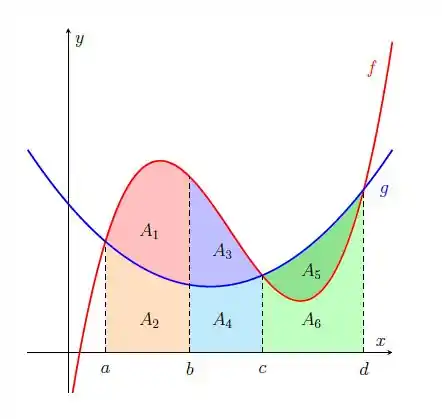
- Escreva o resultado das integrais em termos das medidas das áreas
Questão 136
2) Esboce a região delimitada pelas curvas e decida se a integração deve ser feita com relação a variável ou . Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área da região.
d)
Ver solução completaQuestão 137
Desenhe o conjunto abaixo e calcule a área:
c) é o conjunto de todos tais que .
Ver solução completaQuestão 138
Desenhe o conjunto abaixo e calcule a área
- é o conjunto do plano limitado pelas retas , pelo eixo e pelo
gráfico de
Ver solução completaQuestão 139
Desenhe o conjunto abaixo e calcule a área
- é o conjunto do plano limitado pelas retas e , pelo eixo e pelo
gráfico de
Ver solução completaQuestão 140
Desenhe o conjunto abaixo e calcule a área:
d) é o conjunto de todos tais que .
Ver solução completaQuestão 141
Questão 3) Calcular a área da região limitada do plano, delimitada pelos gráficos das seguintes funções: , e .
Ver solução completaQuestão 142
Considere as funções e . Calcule a área da região delimitada pelos gráficos de e
Ver solução completaQuestão 144
4 – Desenhe no plano cartesiano a região plana dada pelo conjunto dos pontos tais que , com , e calcule sua área.
Ver solução completaQuestão 145
2 – Calcule, com detalhes, a área da região de uma “pétala” da rosácea de três “pétalas” dada pela equação .

Questão 148
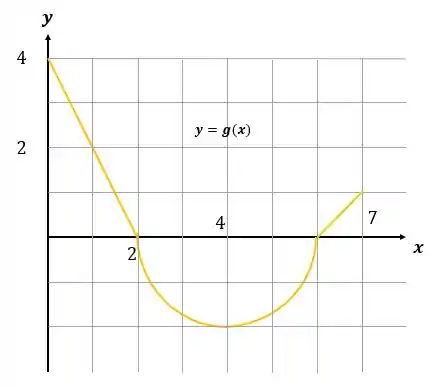
O gráfico de consiste de dois segmentos de retas e um semi-circulo, conforme a figura abaixo.
Calcule:
a)
b)
c)
Questão 149
Considere as curvas e .
- Esboce as curvas acima em um mesmo plano cartesiano exibindo os pontos de intersecção com suas abscissas e ordenadas.
- Exiba uma ou mais integrais que determinem a área da região delimitada por estas curvas.
- Calcule a área desta região.
Questão 151
Considere a região plana
a) Esboce abaixo a região .
b) Escreva a área da região através de uma soma de integrais na variável . Atenção: Neste item não é necessário calcular as integrais.
Ver solução completaQuestão 152
Sabendo que
É a equação de uma circunferência de centro e raio , considere a região plana
- Esboce abaixo a região . Indique explicitamente em seu desenho as coordenadas de três pontos que pertençam à fronteira da região.
- Calcule a área da região utilizando o método que preferir.
Questão 153
Sejam um número real positivo e a região limitada pelas retas e e os eixos e , no primeiro quadrante do plano cartesiano. Sabe-se que a área da região é igual a . O valor de é
Ver solução completa
Questão 154
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região
(1) , ,
Ver solução completaQuestão 155
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região
(4) , ,
Ver solução completaQuestão 156
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região
(3) , ,
Ver solução completaQuestão 157
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e sua largura. Então, calcule a área da região.
Ver solução completa
Questão 158
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e sua largura. Então, calcule a área da região.
Ver solução completa
Questão 159
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região
(12), , ,
Ver solução completaQuestão 160
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região
(8) , ,
Ver solução completaQuestão 161
Calcule a área da região delimitada pela função e o eixo no intervalo .
Ver solução completaQuestão 162
A área da região sob o gráfico de função
acima do eixo , entre as retas e , é:
Ver solução completaQuestão 163
Repita o argumento acima para as funções abaixo. Neste caso, você encontrará 3 raízes para a equação , digamos . A área agora será calculada como a soma de duas integrais, uma do tipo e outra . Em cada uma delas, você deve integrar a função que está por cima, menos a que está por baixo do intervalo de integração
Ver solução completaQuestão 164
Determine a área da região plana delimitada pela curva e por sua reta tangente no ponto de abscissa
Ver solução completaQuestão 166
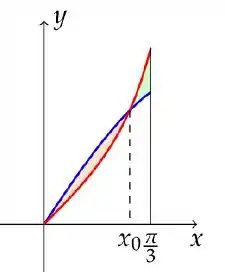
Determine o valor de para o qual o ponto de insterseção dos gráficos das funções definidas no intervalo , divida a região entre eles em duas regiões de mesma área. Vide figura abaixo.
Questão 167
Q02) Considere com
a) Determine o domínio, a imagem e a expressão da função (a função inversa de )
b) Esboce abaixo os gráficos das funções e
c) Considere a região plana definida abaixo:
c.1) Seja a abscissa do único ponto de interseção entre os gráficos das funções e . Escreva a área de como uma soma de integrais na variável
c.2) Calcule a área da região em termos de
Ver solução completaQuestão 168
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região
(1) , ,
Ver solução completaQuestão 169
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região
(6) , ,
Ver solução completaQuestão 173
Calcular a área das seguintes regiões :
b) delimitada pelas curvas e .
Ver solução completaQuestão 174
Proceda como no exercício anterior para calcular a área da região limitada pelas curvas dadas:
Ver solução completaQuestão 175
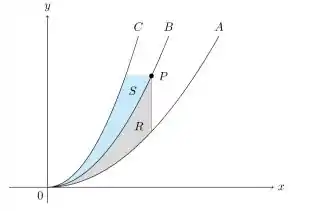
Considere as curvas , e , no primeiro quadrante do plano cartesiano, e as regiões S e R indicadas na figura abaixo. Sabe-se que para todo , a razão entre as áreas das regiões S e R é igual a 5. Quanto vale 25a?
Questão 176
Questão 4
Seja a região limitada pela curva e pelas retas , e .
a) Faça um esboço da região
b) Determine a área de
c) Calcule o volume obtido pela rotação da região em torno do eixo .
Ver solução completaQuestão 177
Encontrar a área da região delimitada pelo laço interno da limaçon . Grafique.
Ver solução completaQuestão 179
Sejam as raízes da função .
Seja a função quadrática cujo gráfico passa pelo ponto e que possui raízes e .
Seja a região delimitada pelos gráficos de e .
a) Determine a expressão da função .
b) Determine o crescimento e o decrescimento de .
c) Faça abaixo um esboço da região . Indique explicitamente em seu desenho as coordenadas (abscissas e ordenadas) de todos os pontos de intersecção entre os gráficos de e .
d) Escreva a área de como uma soma de duas integrais na variável .
Ver solução completaQuestão 180
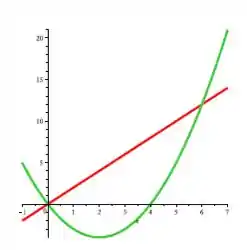
Se e são funções contínuas e em , então a área da região compreendida acima do gráfico de e abaixo do gráfico de é dada por . Nos itens abaixo, vamos calcular esta área para o caso em que e
- Determine as soluções da equação , chamando de o menor valor e o maior.
- Pelo Teorema do Valor Intermediário temos que, em todo intervalo , uma das funções é sempre maior ou igual a outra. Determine qual delas é a maior, calculando cada uma delas em um ponto e comparando os dois valores
- Determine agora a área integrando, no intervalo , a função que está por cima menos a que está por baixo
Questão 181
Repita o argumento acima para as funções abaixo. Neste caso, você encontrará 3 raízes para a equação , digamos . A área agora será calculada como a soma de duas integrais, uma do tipo e outra . Em cada uma delas, você deve integrar a função que está por cima, menos a que está por baixo do intervalo de integração
Ver solução completaQuestão 182
Seja Considere a região plana
b) Esboce abaixo a região . Indique em seu desenho as coordenadas dos pontos de interseção
do gráfico de com os eixos e .
c) Escreva a área de como uma integral na variável .
d) Escreva a área de como uma integral na variável .
e) Calcule a área de .
Ver solução completaQuestão 184
Sejam as curvas e desenhadas em anexo. Formule, em cada caso, uma integral para calcular:
b) A área exterior à rosa e interior ao círculo .
Ver solução completaQuestão 186
Considere a integral
(1) Desenhe a região de integração. Justifique.
(2) Trocando a ordem de integração, calcule a integral .
Ver solução completaQuestão 189
2) Esboce a região delimitada pelas curvas e decida se a integração deve ser feita com relação a variável ou . Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área da região.
c)
Ver solução completaQuestão 190
Esboce a região delimitada pelas curvas e decida se a integração deve ser feito com relação a variável x ou y. Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área de integração.
g)
Ver solução completaQuestão 191
2) Esboce a região delimitada pelas curvas e decida se a integração deve ser feita com relação a variável ou . Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área da região.
e)
Ver solução completaQuestão 194
Seja a região plana dada pelo esboço abaixo:
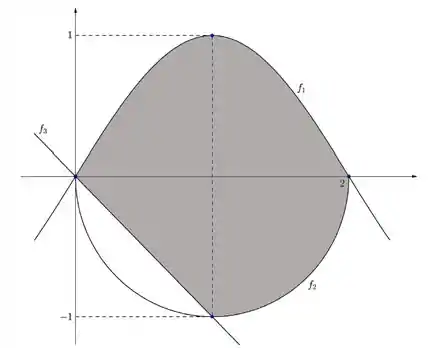
Onde ,e são funções tais que:
- , com uma constante
- O gráfico de é uma semicircunferência com máximo nos pontos e
- O gráfico de é uma reta que passa pela origem e pelo ponto de mínimo da função
- Determine a expressão das funções ,e
- Escreva a área da região como uma soma de duas integrais na variável
- Calcule a área da região
Questão 195
Seja a região de interseção das curvas e . Esboce a região e calcule sua área.
Ver solução completaQuestão 196
Sejam as curvas e desenhadas em anexo. Formule, em cada caso, uma integral para calcular:
a) A área fora do círculo e interior à rosa.
Ver solução completaQuestão 198
2) Esboce a região delimitada pelas curvas e decida se a integração deve ser feita com relação a variável ou . Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área da região.
a) , , ,
Ver solução completaQuestão 199
5. A figura 1 representa o gráfico de uma função definida no intervalo . Calcule as integrais abaixo:
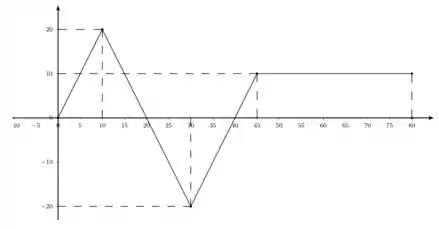
c)
d)
Ver solução completaQuestão 200
5. A figura 1 representa o gráfico de uma função definida no intervalo . Calcule as integrais abaixo:
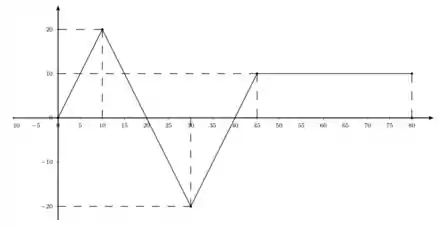
a)
b)
Ver solução completaQuestão 201
5. A figura 1 representa o gráfico de uma função definida no intervalo . Calcule as integrais abaixo:
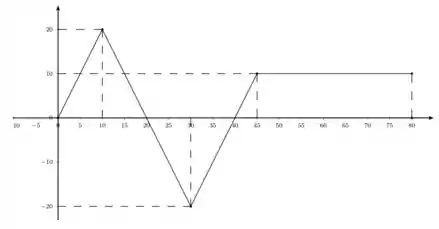
e)
f)
Ver solução completaQuestão 202
Questão 3:
Sejam e funções dadas por
e
e considere a região dada por
- Esboce a região .
- Escreva a área da região como uma soma de duas integrais na variável .
- Escreva a área da região como uma soma de duas integrais na variável .
- Calcule a área da região .
Questão 203
Esboce a curva e calcule a área da região indicada:
a) a região limitada por um laço de rosácea
Ver solução completaQuestão 204
Determine o volume da região interior à esfera e exterior ao cilindro , com .
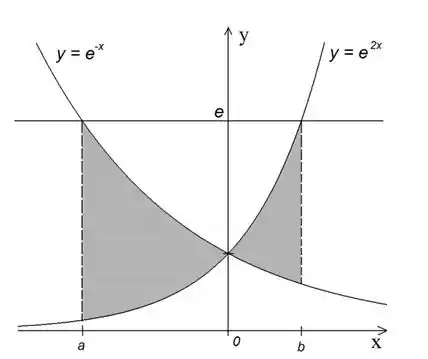
Ver solução completaQuestão 206
Determine o valor de e e calcule a área da região destacada na figura abaixo:
Questão 207
Calcule a área da região limitada pelas curvas e . Faça um esboço da região.
Ver solução completaQuestão 208
Na figura abaixo está o gráfico de .
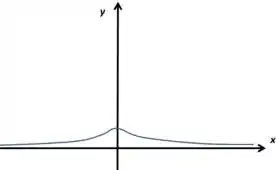
Seja . Desenhe a região compreendida entre os gráficos de e e as retas e . Calcule a sua área.
Ver solução completaQuestão 213
Proceda como no exercício anterior para calcular a área da região limitada pelas curvas dadas:
Ver solução completaQuestão 214
Esboce a curva e calcule a área da região indicada:
b) a região limitada pela lemniscata
Ver solução completaQuestão 215
Seja a região do plano interior ao cardióide e exterior ao círculo . Calcule:
Ver solução completaQuestão 217
Ache o núumero b tal que a reta divida a região delimitada pelas curvas e em duas regiões de áreas iguais.
Ver solução completaQuestão 218
Considere a função definida por , divida o intervalo em partes iguais como o indicado na figura abaixo e resolva os itens a seguir.
Defina, para cada , o ponto e calcule .
Defina agora e calcule
Usando a seguinte formula:
Lembrando que a integral e o limite, quando , do somatório em (1), encontre a área delimitada pelo gráfico da função e o eixo .
Ver solução completaQuestão 219
A figura ao lado indica a área delimitada pelos gráficos das funções
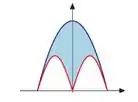
E
Com . Use a integral definida para calcular o valor dessa área.
Ver solução completaQuestão 220
Seja a região limitada pelos eixos e pelo arco de parábola , para entre e .
a) Calcule a área da região
Ver solução completaQuestão 222
Determine a área da região limitada pelas curvas dadas em cada caso:
a) , , e
Ver solução completaQuestão 223
Determine a área da região limitada pelas curvas dadas em cada caso:
d) , e
Ver solução completaQuestão 224
Determine a área da região limitada pelas curvas dadas em cada caso:
b) , e
Ver solução completaQuestão 225
Calcule a área da intersecção das regiões limitadas pelas curvas dadas em coordenadas polares.
- e
Questão 226
Calcule a área da intersecção das regiões limitadas pelas curvas dadas em coordenadas polares.
(b) e
Ver solução completaQuestão 227
Calcule a área da intersecção das regiões limitadas pelas curvas dadas em coordenadas polares.
(c) e
Ver solução completaQuestão 228
Calcule a área da intersecção das regiões limitadas pelas curvas dadas em coordenadas polares.
(e) e
Ver solução completaQuestão 229
Calcule a área da intersecção das regiões limitadas pelas curvas dadas em coordenadas polares.
(d) e
Ver solução completaQuestão 230
Calcule a área do conjunto de todos os pontos tais que (coordenadas polares).
Ver solução completaQuestão 231
Calcule a área da região situada no 1º quadrante, limitada acima pela curva (coordenadas cartesianas) e abaixo por (coordenadas polares), com .
Ver solução completaQuestão 236
Considere a região delimitada pelas curvas e
Esboce a região .
Calcule a área da região .
Ver solução completaQuestão 237
Use o Cálculo para encontrar a área do triângulo cujos vértices são e .
Ver solução completaQuestão 238
Seja diferenciável. Calcule
Sabendo que e que
É igual a área da região entre o gráfico de e as retas , e
Ver solução completaQuestão 240
Deseja-se calcular a área sob o gráfico da função para
- Explique, por meio de um teorema, por que utilizamos uma primitiva da função para o cálculo da área sob seu gráfico.
- Utilize a substituição e reescreva a integral apenas em termos da variável .
- Utilize a substituição e reescreva a integral apenas em termos da variável .
- Escolha um dos itens acima para determinar a área desejada.
Questão 241
Esboce e calcule a área da região do plano- determinada pelas inequações:
b)
e
Ver solução completaQuestão 242
Esboce e calcule a área da região do plano- determinada pelas inequações:
a)
e
Ver solução completaQuestão 243
Determine a equação da reta passando por , tal que a área da região limitada por e pela curva , com , seja igual a .
Ver solução completaQuestão 244
Considere a região delimitada pelas curvas e ,
Esboce a região .
Determine uma integral ou soma de integrais em que represente a área desta região.
Determine uma integral ou soma de integrais em que represente a área desta região
Calcule a área da região .
Ver solução completaQuestão 245
Proceda como no exercício anterior para calcular a área da região limitada pelas curvas dadas:
Ver solução completaQuestão 246
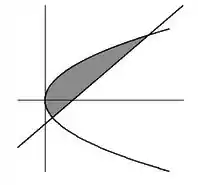
Sabendo que:
- A parábola possui vértice na origem e passa pelo ponto
- A reta passa pelos pontos e
- Determine a equação da parábola e a equação da reta
- Descreva a região através de um conjunto de desigualdades
- Escreva a área da região através de uma integral ou de uma soma de integrais (Não é necessário calcular a integral)
- Calcule a área da região
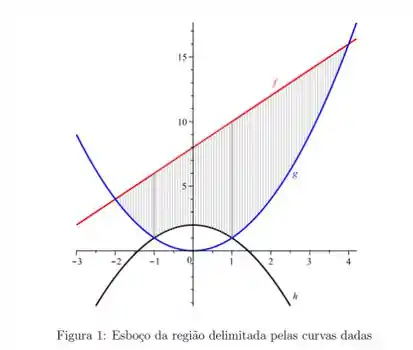
Questão 247
Determine a área da região limitada exatamente pelas três curvas
Questão 248
Considere as funções e . Esboce e calcule a área da região limitada pelos gráficos de e no intervalo .
Ver solução completaQuestão 249
Considere as funções e . Esboce e calcule a área da região limitada pelos gráficos de e no intervalo .
Ver solução completaQuestão 256
Esboce a região limitada pelas curvas e e em seguida calcule a área desta região.
Ver solução completaQuestão 257
Considere a região plana
- Esboce a região
- Escreva a área da região como uma soma de duas integrais na variável . Atenção Neste item não é necessário calcular as integrais.
- Escreva a área da região como uma soma de três integrais na variável . Atenção Neste item não é necessário calcular as integrais.
- Calcule a área da região
Questão 258
- Determine os valores de para os quais
- Sejam e os valores encontrados no item , determine a equação da parábola que tem vértice em e cujos pontos de interseção com o eixo são e
- Esboce a região abaixo onde é a função determinada no item e e são os valores encontrados no item
- Calcule a área da região
Ver solução completaQuestão 259
Determine a área da superfície:
- A parte do plano que está dentro do cilindro
Questão 260
Determine a área da superfície:
- A parte do cone que se encontra entre o plano e o cilindro
Questão 261
Considere a região destacada na figura abaixo que é delimitada pelas curvas e .
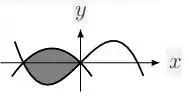
A área de é dada por:
Questão 262
Na figura abaixo, sabendo que , determine os valores de e e calcule a área da região destacada.
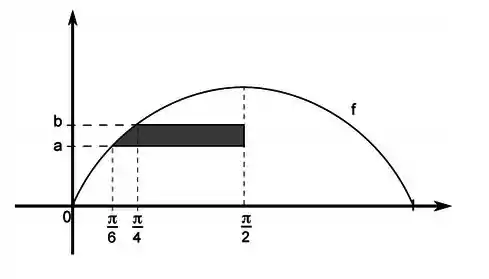
Questão 263
Considere a região plana limitada pelas curvas , e :
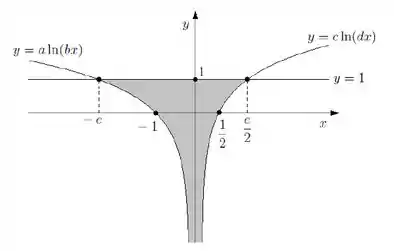
- Utilizando as informações fornecidas no esboço acima, determine o valor das constantes , , , .
- Escreva a área de como uma integral ou uma soma de integrais na variável
- Escreva a área de como uma integral ou uma soma de integrais na variável
- Calcule a área de pelo método que preferir
Questão 264
Faça um esboço da região R limitada pelas curvas e calcule sua área.
Ver solução completaQuestão 266
Esboce e calcule a área da região do plano- determinada pelas inequações:
c)
e
Ver solução completaQuestão 267
Esboce e calcule a área da região do plano- determinada pelas inequações:
e)
e
Ver solução completaQuestão 268
Esboce e calcule a área da região do plano- determinada pelas inequações:
f)
e
Ver solução completaQuestão 270
Esboce e calcule a área da região do plano- determinada pelas inequações:
g)
e
Ver solução completaQuestão 271
Esboce e calcule a área da região do plano- determinada pelas inequações:
d)
e
Ver solução completaQuestão 272
Esboce e calcule a área da região do plano- determinada pelas inequações:
h)
e
Ver solução completaQuestão 276
A reta horizontal intercepta a curva no primeiro quadrante como mostra a figura.
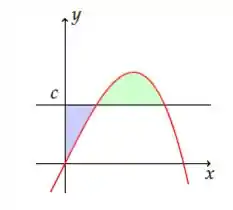
Determine para que as áreas das duas regiões sombreadas sejam iguais.
Ver solução completaQuestão 277
Questão 3. Sejam as curvas e desenhadas em anexo. Formule, em cada caso, uma integral para calcular:
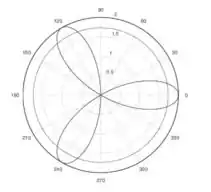
c) A área da região interior a ambas as curvas
Ver solução completaQuestão 278
Questão 2. Dados os gráficos de , e as regiões , , , e , delimitadas seguem a figura anexa, formule, em cada caso, a integral que calcula o volume do sólido obtido ao girar a região indicada ao redor do eixo apontado.
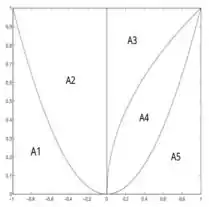
a) ao redor da reta .
Ver solução completaQuestão 279
Questão 3. Sejam as curvas e desenhadas em anexo. Formule, em cada caso, uma integral para calcular:

a) A área da região interior a ambas as curvas
Ver solução completaQuestão 280
Questão 3. Sejam as curvas e desenhadas em anexo. Formule, em cada caso, uma integral para calcular:
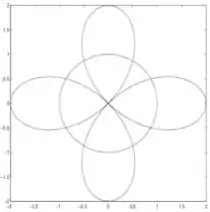
b) A área fora do círculo e interior à rosa.
Ver solução completaQuestão 281
Questão 2. Dados os gráficos de , e as regiões , , , e , delimitadas seguem a figura anexa, formule, em cada caso, a integral que calcula o volume do sólido obtido ao girar a região indicada ao redor do eixo apontado.
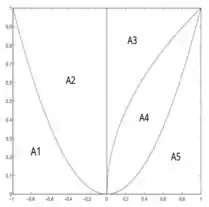
b) ao redor de .
Ver solução completaQuestão 282
Questão 2. Dados os gráficos de , e as regiões , , , e , delimitadas seguem a figura anexa, formule, em cada caso, a integral que calcula o volume do sólido obtido ao girar a região indicada ao redor do eixo apontado.
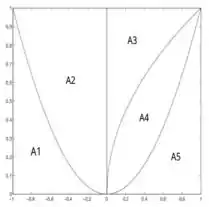
c) ao redor de .
Ver solução completaQuestão 283
As regiões A, B e C da figura são limitadas pelo gráfico de f e pelo eixo x. Se a área de cada
região vale . (unidades de área), qual é o valor de ?
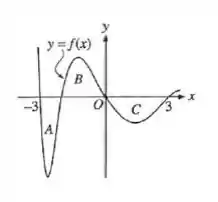
Questão 284
- Se é o segmento de reta ligando o ponto ao ponto , mostre que
- No sentido anti-horário, os vértices de um polígono são Mostre que sua área é dada por:
Questão 287
Esboce a região correspondente a cada uma das integrais definidas, depois calcule as integrais.
c)
Ver solução completaQuestão 288
Encontre a área da região limitada pelo gráfico de , o eixo dos e as retas verticais e .
(Obs: Antes de resolver a integral, faça um esboço do gráfico, para verificar a região a ser calculada).
Ver solução completaQuestão 289
Esboce a região correspondente a cada uma das integrais definidas, depois calcule as integrais.
b)
Ver solução completaQuestão 290
Esboce a região correspondente a cada uma das integrais definidas, depois calcule as integrais.
d)
Ver solução completaQuestão 291
Calcule o comprimento do astróide definido pelas seguintes equações paramétricas:
Ver solução completaQuestão 292
EE3. 2017.1 Esboce a região limitada pelas curvas e e em seguida calcule a área da região.
Ver solução completaQuestão 293
Calcule a área da região que não contém a origem, sendo limitada pela rela e pela circunferência .
Ver solução completaQuestão 294
Seja o conjunto do plano limitado pela reta e pelo gráfico de , com . Desenha e calcule sua área.
Ver solução completaQuestão 297
11.4 Seja a região limitada pelos gráficos de e para e o sólido obtido pela revolução desta área em torno do eixo .
a) Calcule a área de
Ver solução completaQuestão 298
10.4 Seja a região limitada por e por , com .
a) Calcule a área de .
Ver solução completaQuestão 299
11.8 Seja a região limitada pelo eixo e pelo gráfico de , com . Seja o sólido obtido ao girarmos em torno do eixo . Encontre a área de e o volume de .
Ver solução completaQuestão 300
10.5 Decida se cada afirmação é verdadeira ou falsa. Justifique as verdadeiras e corrija adequadamente as falsas.
a) A integral
Calcula a área da região limitada pelo gráfico de e o eixo , com .
Ver solução completaQuestão 302
Encontre a área da região limitada pela curva nos setores indicados:
b)
Ver solução completaQuestão 303
Seja a função definida no disco unitário e seja o gráfico da função . Ache a área de .
Ver solução completaQuestão 304
Calcule a área da região situada entre o eixo e o gráfico da função com no intervalo

Questão 310
Para cada , seja a área delimitada pelas curvas e , com .
a) Calcule .
b) Determine para que seja mínima.
Ver solução completaQuestão 311
1 - Determine a área da região limitada pelas curvas dadas em cada caso
c) e
Ver solução completaQuestão 315
Calcule a área da superfície gerada pela rotação, em torno do eixo , da curva , com .
Ver solução completaQuestão 317
Calcule a área da região do plano compreendida entre as seguintes curvas:
Ver solução completaQuestão 318
- Se é o segmento de reta ligando o ponto ao ponto , mostre que
- No sentido anti-horário, os vértices de um polígono são Mostre que sua área é dada por:
Questão 319
- Se é o segmento de reta ligando o ponto ao ponto , mostre que
- No sentido anti-horário, os vértices de um polígono são Mostre que sua área é dada por:
- Determine a área do pentágono de vértices .
Questão 320
Considera-se a área entre a curva e o eixo para .
a) Determinar a medida de e as coordenadas do centroide .
Ver solução completaQuestão 321
Considere a região R delimitada pelas curvas y = x², y = 0 e x = 1. Faça um esboço da região R e encontre o volume do sólido obtido pela rotação da região R ao redor de x = 2.
Ver solução completaQuestão 322
Final. 2019.2 Esboce as regiões do plano delimitadas pelos gráficos de e e e calcule a área desta região.
Ver solução completaQuestão 323
EE3. 2019.1 Esboce as regiões do plano delimitadas pelos gráficos de e e e calcule sua área.
Ver solução completaQuestão 324
EE3. 2019.1 Esboce as regiões do plano delimitadas pelos gráficos de e pelo semicírculo superior de raio centrado na origem.
Ver solução completaQuestão 325
EE3. 2019.2 Esboce as regiões do plano delimitadas pelos gráficos de e e calcule a área de cada uma dessas regiões.
Ver solução completaQuestão 327
EE3. 2017.2 Sabe-se que as curvas e intersectam-se em exatamente três pontos com abscissas e, respectivamente, onde número é um real negativo. Calcule a área total, em termos de , da região entre .
Ver solução completaQuestão 328
EE3. 2015.2 Considere a região no primeiro quadrante limitada pelas curvas , e . Esboce a região e calcule sua área.
Ver solução completaQuestão 329
EE3. 2012.2 Esboce a região do plano delimitada pela parábola , pela reta e pelo eixo .
Ver solução completaQuestão 330
EE3. 2012.1 Esboce a região delimitada pelas curvas e e calcule o valor numérico de sua área.
Ver solução completaQuestão 331
Final. 2011.2 Seja Encontre a área da região delimitada pelo gráfico de , pelo eixo e pelas retas e .
Ver solução completaQuestão 333
Esboce a região limitada pelas curvas indicadas e encontre sua área:
Ver solução completaQuestão 334
Esboce a região limitada pelas curvas indicadas e encontre sua área:
Ver solução completaQuestão 335
Em cada item, determine a área da região delimitada pelos gráficos das curvas.
e) , e .
Ver solução completaQuestão 336
Represente a área da região por uma integral:
é a região no primeiro quadrante limitada pelo eixo , pela reta e pelo círculo .
Ver solução completaQuestão 337
Represente a área da região por uma integral:
é a região de intersecção dos círculos e
Ver solução completaQuestão 338
Determine de modo que a área da região acima da reta e abaixo da parábola seja .
Ver solução completaQuestão 339
Considere o triângulo de vértices (0, 4), (2, −2) e (4, 0). Faça um esboço do triângulo e utilize integral para calcular sua área.
Ver solução completaQuestão 341
Esboce a região limitada pelas curvas indicadas e encontre sua área:
Ver solução completa
Questão 342
Encontre o número tal que a reta divida a região limitada pelas curvas e em duas regiões com áreas iguais. (Dica:
Ver solução completaQuestão 344
10.4 Seja a região limitada por e por , com .
c) Seja o sólido gerado pela rotação de em torno do eixo . Qual o volume de ?
Ver solução completaQuestão 345
Esboce a região limitada pelas curvas indicadas e encontre sua área:
Ver solução completaQuestão 346
Encontre a área da região limitada pela parábola , pela reta tangente a esta parábola em e pelo eixo .
Ver solução completaQuestão 347
10.4 Seja a região limitada por e por , com .
b) Seja o sólido gerado pela rotação de em torno do eixo . Calcule o volume de .
Ver solução completaQuestão 348
Encontre a área da região limitada pela curva nos setores indicados:
a)
Ver solução completaQuestão 352
Encontre os valores de tais que a área da região delimitada pelas parábolas e seja .
Ver solução completaQuestão 353
Esboce a região limitada pelas curvas indicadas e encontre sua área:
Ver solução completaQuestão 355
Esboce a região limitada pelas curvas indicadas e encontre sua área:
Ver solução completaQuestão 357
Encontre o volume do sólido pela rotação ao redor do eixo x da região determinada pelas curvas com . Faça um esboço da região.
Ver solução completaQuestão 358
Use a integral dupla para calcular a área da região D limitada pelas curvas
Ver solução completaQuestão 359
- Esboce a região do plano delimitada pela parábola , pela reta e pelo eixo .
- Calcule o valor da área da região .
Ver solução completaQuestão 360
Seja a região do plano delimitada inferiormente pelo eixo , superiormente pelo gráfico de , à esquerda pela reta e à direita pela reta .
Se a area , entao
Questão 361
Q01) Seja a região plana dada por:
- Esboce abaixo a região . Indique explicitamente em seu desenho as coordenadas de três pontos que pertençam à fronteira da região.
- Escreva a área da região através de uma soma de duas integrais na variável . Atenção: Neste item não é necessário calcular as integrais.
- Escreva a área da região através de uma soma de duas integrais na variável . Atenção: Neste item não é necessário calcular as integrais.
- Calcule a área da região utilizando o método que preferir.
Questão 362
A reta de equação divide a região compreendida entre as parábolas de equações e em duas partes. Mostre que as áreas das regiões obtidas são iguais e calcule o seu valor.
Ver solução completaQuestão 363
Seja a região plana dada por
a) Esboce a região Indique explicitamente os pontos de interseção entre as curvas.
b) Escreva a área da região através de uma integral na variável
c) Calcule a área da região
Ver solução completaQuestão 364
Seja a região plana dada por
- Esboçe abaixo a Região Indique explicitamente em seu desenho as coordenadas dos seguintes pontos:
- Vértice da parábola
- Ponto de interseção da parábola com o eixo
- Ponto de interseção entre as duas retas
Atenção: Neste item não é necessário calcular as integrais
Atenção: Neste item não é necessário calcular as integrais
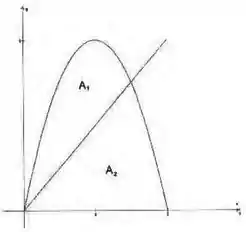
Questão 365
Seja e considerar a reta de equação , . Determine o valor de para o qual as áreas e mostradas na figura são iguais.
Questão 367
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região
(10) ,
Ver solução completaQuestão 368
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e sua largura. Então, calcule a área da região.
Ver solução completa
Questão 369
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região
(8) , ,
Ver solução completaQuestão 370
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região
(9) , , ,
Ver solução completaQuestão 371
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região
(3) , ,
Ver solução completaQuestão 372
Seja A a área da região limitada pelas curvas e . O valor de 12A é quanto?
Ver solução completaQuestão 374
Desenhe o conjunto abaixo e calcule a área
- é o conjunto do plano limitado pelas retas , pelo eixo e pelo
gráfico de
Ver solução completaQuestão 375
Desenhe o conjunto abaixo e calcule a área:
d) é o conjunto de todos tais que .
Ver solução completaQuestão 376
Esboce a região delimitada pelas curvas e decida se a integração deve ser feito com relação a variável x ou y. Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área de integração.
h)
Ver solução completaQuestão 377
Desenhe o conjunto A abaixo e calcule a área:
e) é um conjunto de todos tais que , com .
Ver solução completaQuestão 378
Desenhe o conjunto abaixo e calcule a área:
c) é o conjunto de todos tais que .
Ver solução completaQuestão 379
Questão 3. Sejam as curvas e desenhadas em anexo. Formule, em cada caso, uma integral para calcular:
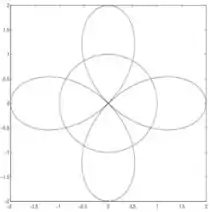
c) A área exterior à cardioide e interior ao círculo.
Ver solução completa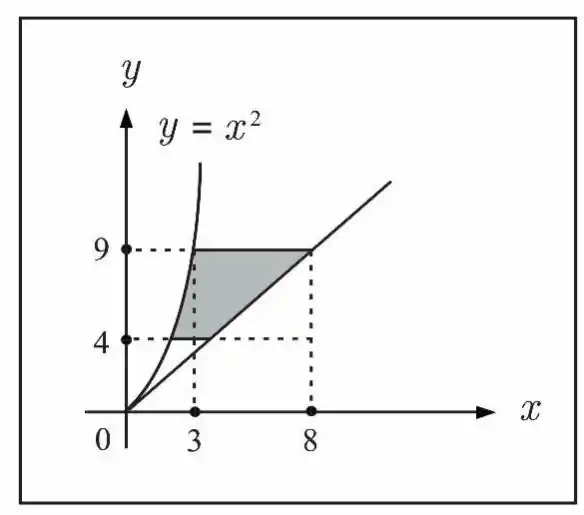
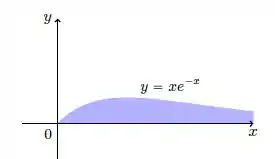
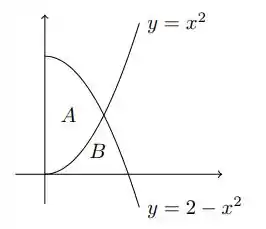
 Calcule a área da região hachurada na figura abaixo
Calcule a área da região hachurada na figura abaixo