Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Exercícios práticos - Ex. 79
Esboce as seções cônicas cujas equações de coordenadas polares são fornecidas nos Exercícios 77-80. Forneça coordenadas polares para os vértices e, no caso de elipses, para os centros também.
Passo 1
Olá galerinha, espero que estejam bem e ansiosos para resolver este exercício comigo! Vamos lá.
Seja um ponto fixado (chamado foco) e uma reta fixada (denominada diretriz) em um plano. Seja um número positivo fixado (conhecido como excentricidade). O conjunto de todos os pontos no plano tal que:
Ou seja, a razão da distância a e da distância a é a constante é uma seção cônica.
A cônica para:
- Elipse ;
- Parábola ;
- Hipérbole .
A seguinte equação polar representa uma seção cônica:
Sabendo disso iremos para nosso exercício no próximo passo.
Passo 2
Do enunciado temos a seguinte Equação:
Podemos observar que a excentricidade é , portanto, representa uma hipérbole. Agora, iremos transformar a equação polar em cartesiana, onde:
Reescrevendo a equação:
Elevando ambos os lados ao quadrado:
Completando o quadrado da equação:
Logo:
Além disso, pela equação sabemos:
Sendo assim, o vértice em coordenadas cartesianas é :
Passo 3
Agora precisamos encontrar as coordenadas polares para cada vértice, para:
- ; :
- ; :
Logo:
Logo:
Então os vértices em coordenadas polares são e .
Passo 4
Usando o programa computacional WolframAlpha, conseguimos esboçar a seguinte curva:
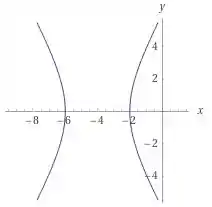
Resposta
e .