Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Exercícios práticos - Ex. 88
Espirais de Arquimedes. O gráfico de uma equação da forma , em que 𝑎 é uma constante diferente de zero, é chamado de espiral de Arquimedes. Existe algo de especial sobre as larguras entre as voltas sucessivas de tal espiral?
Passo 1
Olá galerinha, tudo bem com vocês? Este é um exercício mais teórico, mas vamos lá!
Primeiramente, pelo enunciado, sabemos que a equação que define a espiral de Arquimedes é:
Onde .
Utilizando o programa computacional WolframAlpha, para , obtemos o seguinte gráfico:
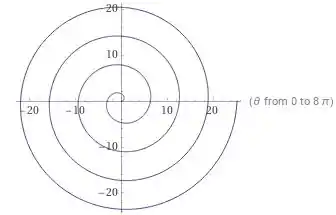
Se você quiser testar diversos valores para irá perceber que sempre terá o mesmo comportamento.
Passo 2
Sendo assim, podemos notar pelo gráfico que as distâncias constantes na espiral de Arquimedes são medidas ao longo dos raios de sua origem, que não atravessam a curva em ângulos retos, enquanto a distância entre as curvas paralelas é medida ortogonalmente a ambas as curvas. E por mais que a espiral de Arquimedes assemelhe-se muito à evolvente de um círculo, ainda assim são ligeiramente diferentes entre si, como podemos observar na seguinte Figura:
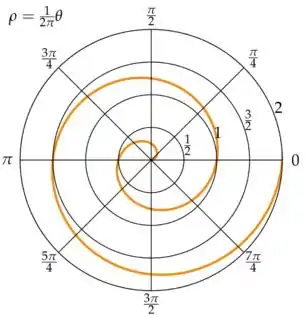
Esse já acabou, até mais pessoal.
Resposta
Resposta no Passo 2.