Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.2 - Ex. 84

Escreva uma equação para a elipse x ² 4 + y ² 25 = 1 transladada 3 unidades para a direita e 2 unidades para baixo. Esboce a elipse e identifique seu centro e seu eixo principal.

Passo 1

Então galera, para iniciar a nossa resolução vamos começar nos atentando a alguns detalhes, beleza? O primeiro detalhe é que para uma elipse com centro ( 0,0 ) a equação na forma padrão é dada por:

x ² a ² + y ² b ² = 1

Assim como discutido na seção 1.2 do George, o gráfico dessa equação para a > b apresenta eixo principal horizontal. Caso contrário, se b > a , o gráfico dessa equação apresenta eixo principal vertical. Em ambos os casos, o eixo principal tem o maior comprimento.

Se escrevermos a equação que nos foi dada dessa forma, teremos:

x ² 2 ² + y ² 5 ² = 1

a = 2 e b = 5

Passo 2

Essas informações obtidas já seriam o suficiente para plotarmos o gráfico da elipse. No entanto, a questão nos diz que a elipse foi transladada 3 unidades para a direita e 2 unidades para baixo. Quando acontece esse tipo de translação, o formato da equação da elipse passa a ser o seguinte:

( x - h ) ² a ² + ( y - k ) ² b ² = 1

No qual agora o centro da elipse deixa de ser ( 0,0 ) e passa a ser ( h , k ) , tranquilo?

A primeira translação é feita para a direita, certo? Então é uma translação feita no eixo x . A segunda translação é feita para baixo, certo? Então é uma translação feita no eixo y . Quando há uma soma diretamente nas variáveis, isso significa que o gráfico da função vai ser deslocado para a esquerda (eixo x ) ou para baixo (eixo y ). Quando há uma subtração diretamente nas variáveis, isso significa que o gráfico vai ser deslocado para a direita (eixo x ) ou para cima (eixo y ).

Como no nosso caso houve uma translação para a direita e outra para baixo, utilizando o raciocínio acima, teremos a equação nesse formato aqui:

( x - 3 ) ² 2 ² + ( y + 2 ) ² 5 ² = 1

( x - 3 ) ² 2 ² + ( y - [ - 2 ] ) ² 5 ² = 1

Passo 3

Agora que temos, de fato, todas as informações para plotarmos o gráfico da elipse, fazendo as translações devidas, o gráfico vai ficar desse jeito, galera:

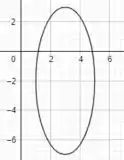
No qual o centro é em ( 3 , - 2 ) e o eixo principal é uma reta que liga os extremos que apresentam maior raio, que nesse caso seria o segmento ( 3,3 ) até ( 3 , - 7 ) . O segmento seria esse aqui:

Resposta

( x - 3 ) ² 2 ² + ( y - [ - 2 ] ) ² 5 ² = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça o gráfico da função y = ( - 5 x ) 1 / 3 sem traçar pontos, mas iniciando com o gráfico de uma das funções padrão apresentadas nas figuras (1), (2) e (3) e aplicando uma transformação apropriada.F
Faça o gráfico da função y = 1 2 x 2 + 1 sem traçar pontos, mas iniciando com o gráfico de uma das funções padrão apresentadas nas figuras (1), (2) e (3) e aplicando uma transformação apropriada.Figur
Faça o gráfico da função y = 1 - x 3 sem traçar pontos, mas iniciando com o gráfico de uma das funções padrão apresentadas nas figuras (1), (2) e (3) e aplicando uma transformação apropriada.Figura (1
Faça o gráfico da função y = - 1 + x 2 sem traçar pontos, mas iniciando com o gráfico de uma das funções padrão apresentadas nas figuras (1), (2) e (3) e aplicando uma transformação apropriada.Figura
A figura a segui mostra o gráfico de y = - x 2 transladado para quatro novas posições. Escreva uma equação para cada novo gráfico.