Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 2.5 - Ex. 5d
Nos exercícios de 2 a 15 :
- Determine os traços
- Determine as seções
- Identifique a superfície quadrica
- Esboce os gráficos
5.
Passo 1
Como vimos nos itens a e b, nos planos XY e XZ temos hipérboles e nenhuma imagem em YZ. E também que se formos olhar as curvas de nível de z (ou seja, fixando valores para z e vendo como a função se comporta em XY)
Vemos que essa hipérbole vai se distanciando cada vez mais da origem. Com isso podemos dizer que o gráfico da nossa quadrica é
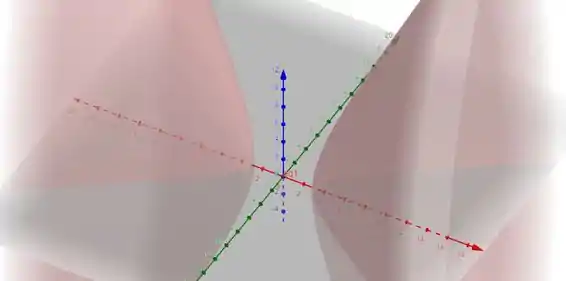
Olhando para o plano XY vemos as hipérboles que havíamos descoberto na função algébrica
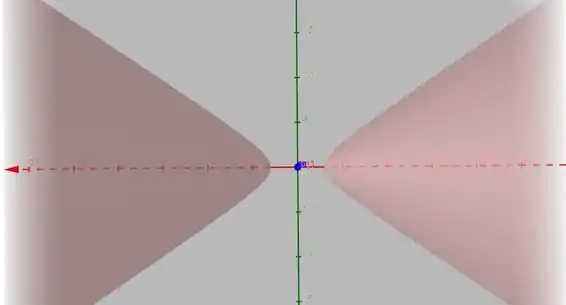
Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos exercícios de 2 a 15 : Determine os traços Determine as seções Identifique a superfície quadrica Esboce os gráficos6. x 2 + 5 y 2 = 8 z 2
Nos exercícios de 2 a 15 : Determine os traços Determine as seções Identifique a superfície quadrica Esboce os gráficos7. z = 4 - 2 x 2 - 3 y 2
Nos exercícios de 2 a 15 : Determine os traços Determine as seções Identifique a superfície quadrica Esboce os gráficos7. z = 4 - 2 x 2 - 3 y 2
Nos exercícios de 2 a 15 : Determine os traços Determine as seções Identifique a superfície quadrica Esboce os gráficos7. z = 4 - 2 x 2 - 3 y 2
Nos exercícios de 2 a 15 : Determine os traços Determine as seções Identifique a superfície quadrica Esboce os gráficos7. z = 4 - 2 x 2 - 3 y 2