Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 7.1 - Ex. 13
Nos Exercícios de 1 a 18, determine se a função é biunívoca. Faça um esboço do gráfico da função.
13.
Passo 1
Primeiro vamos entender o que é uma função biunívoca (ou injetora). Uma função dessa forma tem a característica de que cada componente do seu domínio só tem um correspondente em sua imagem. O diagrama a seguir demonstra essa característica.
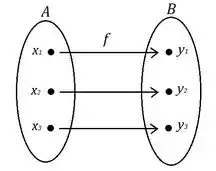
Onde A é o domínio da função e B é a imagem dessa função, pode – se reparar que cada membro do domínio corresponde a um único membro da imagem.
Podemos entender como o domínio da nossa função, onde ela só é definida nesse domínio.
Passo 2
Agora vamos avaliar a função que nos foi dada.
Para fazer isso, vamos usar o teorema 7.1.2 do capítulo 7, seção 2, que diz que se uma função for crescente ou decrescente em todo seu domínio ou intervalo, ela é biunívoca.
Para saber se a função é crescente ou decrescente vamos derivar a função e ver se ela é negativa no seu domínio ou positiva.
Passo 3
Vamos derivar a função.
Passo 4
Agora, sabemos que:
E a função é positiva no intervalo logo é positiva nesse intervalo.
A função negativa no intervalo logo é negativa nesse intervalo.
Vamos discutir sobre a tangente.
A função é positiva no intervalo e no intervalo .
Então a multiplicação da função tangente pela função secante que no caso é a derivada que queremos avaliar resulta que a é positiva em e negativa em .
Logo a função é crescente em e decrescente em .
Assim, a função não assume mesmos valores na imagem com mesmo elemento do domínio, logo ela é biunívoca.
Passo 5
Agora vamos ver como ficaria o gráfico dessa função.
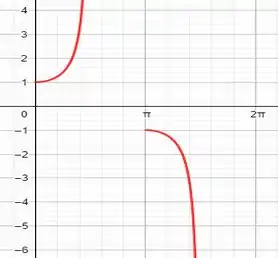
Através do gráfico também é possível ver o que constatamos no passo 4.
Resposta
A função é biunívoca.