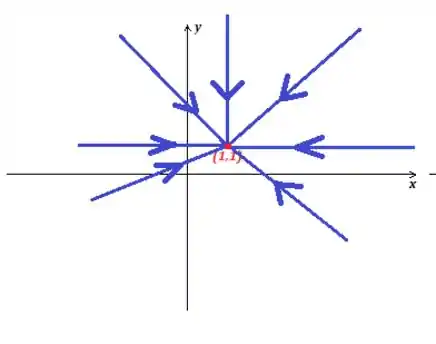
4 - Faça um esboço das trajetórias das soluções para suficientemente grande:
Passo 1
Essas equações são equações independentes entre si, então podemos resolvê-las separadamente!
PRIMEIRA EQUAÇÃO:
Primeiro, vamos encontrar a resposta da homogênea:
Ora, essa equação dá para saber a resposta sem mesmo resolver, né? Quem é a função cuja derivada é ela mesma com o sinal trocado?
Agora vamos encontrar a resposta da particular por variação de parâmetros. Se a função que a torna não homogênea é , uma constante, então essa será a solução particular também, ou seja, uma constante:
Derivando...
Agora substituindo na EDO...
Então a solução geral para será:
Passo 2
SEGUNDA EQUAÇÃO:
POW! Essa equação é parecida com a primeira, então ela vai ter a mesma solução:
A diferença vai ser na constante já que as duas equações são independentes, e podem ser números diferentes também, saca?
Passo 3
Beleza, então as duas respostas em função do tempo são:
Beleza, então, aplicando em todo mundo...
E igualando ambas equações...
Isolando em função de , obteremos...
RETAS!!! De diferentes angulações!
Passo 4
Por outro lado... As duas respostas em função do tempo são:
Poxa, ambas as equações, com muito próximo do infinito, as exponenciais serão basicamente , e as soluções vão tender a:
Isso significa que as soluções são retas de diferentes de diferentes angulações, mas todas as retas tendem ao mesmo ponto final: . Veja o gráfico...
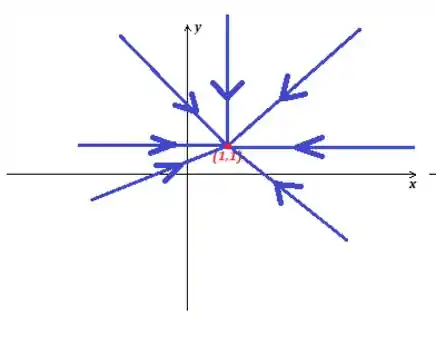
Resposta