Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 17.2 - Ex. 12
Faça o gráfico da solução particular e de várias outras soluções. Que características essas soluções têm em comum?
Passo 1
Olá, tudo bem? Essa é uma equação diferencial de segunda ordem com coeficientes constantes e não homogênea, ou seja, o lado direito da equação não é zero. A solução geral vai ser a combinação linear da parte homogênea e a parte particular :
Passo 2
Vamos primeiro encontrar a solução da parte homogênea. A equação diferencial homogênea associada é:
E supor uma solução do tipo:
O processo para determinar é sempre o mesmo: derivar uma e depois duas vezes e substituir na equação. Vamos lá?
As derivadas:
Agora vamos substituir na equação diferencial:
Dividindo essa equação por temos:
Para resolver essa equação vou usar a fórmula de Bháskara:
Aqui temos duas raízes reais e distintas, então a solução complementar vai ser uma combinação linear de duas exponenciais:
Passo 3
Nesse caso temos duas soluções particulares. Vamos começar com a primeira.
A solução particular vai ser determinada pelo método dos coeficientes indeterminados. A função é , e não faz parte da solução da equação homogênea (ou também chamada de complementar), então uma possível solução vai ser uma constante:
Definida a solução tentativa, agora o procedimento é padrão: derivar uma e duas vezes a função , substituir na equação diferencial completa e igualar os coeficientes. Vamos lá?
As derivadas vão ser:
Resgatando a equação diferencial integral temos:
Agora substituindo e na equação diferencial temos:
E a primeira solução particular é:
Passo 4
A segunda solução particular vai ser dada a partir da função é e também não faz parte da solução da equação homogênea (ou também chamada de complementar), então uma possível solução vai ser uma combinação de seno e cosseno:
As derivadas vão ser:
Resgatando a equação diferencial integral temos:
Agora substituindo e na equação diferencial temos:
Reorganizando os termos temos:
Igualando os coeficientes dos dois lados ficamos com o seguinte sistema:
Isolando da primeira equação vamos ter:
E substituindo na segunda temos o valor de :
Agora substituindo na expressão para :
E a solução particular é:
Passo 5
Show! Agora é só juntar todos os resultados! Do passo temos a solução e dos passos e temos . Vai lá ao passo e pega a solução geral:
Substituindo os resultados teremos:
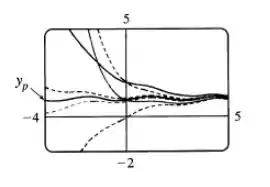
Agora vamos ver um gráfico de várias soluções, mudando os coeficientes:
No limite quando , todas as soluções tentem à solução particular.
Por enquanto é isso pessoal, espero ter ajudado ;)
Beleza?
Vamos pra próxima?