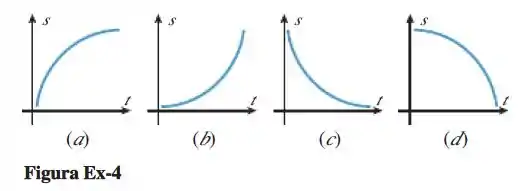
As figuras abaixo mostram as curvas de posição versus tempo para quatro partículas diferentes em movimento retilíneo. Para cada partícula, determine se a velocidade instantânea está aumentando ou diminuindo com o tempo.

Na letra b) a velocidade instantânea está aumentando com o tempo, porque as linhas tangentes se tornam mais íngremes, ou seja, a inclinação vai aumentando à medida que o tempo vai aumentando indicando que a velocidade aumenta.

Na letra c) a velocidade instantânea está aumentando com o tempo, a inclinação começa muito negativa e à medida que o tempo vai aumentando, ela se torna menos negativa, ou seja, a inclinação vai aumentando à medida que o tempo vai aumentando indicando que a velocidade aumenta.

Na letra d) a velocidade instantânea está diminuindo com o tempo, a inclinação começa um pouco negativa e à medida que o tempo vai aumentando, ela se torna mais negativa, ou seja, a inclinação vai diminuindo à medida que o tempo vai aumentando indicando que a velocidade diminui.