A um fio muito leve de comprimento está pendurada uma partícula de massa . Tal partícula é afastada da vertical e abandonada.
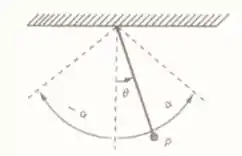
Desprezando-se a resistência do ar, mostra-se em física que o movimento da partícula é regido pela equação
Onde é a aceleração gravitacional supostamente constante. Admita que no instante , , , e . Mostre que o tempo gasto pela partícula para sair da posição e atingir a posição pela primeira vez é
Passo 1
Baseando no
Temos:
Multiplicando por:
Assim:
Logo, existe uma constante tal que, para todo :
Pelas condições iniciais e , temos:
Então:
Passo 2
Desse modo, temos que:
Separando as variáveis:
Passo 3
Calculando :
Então: