A função , , aparece em aplicações a síntese de modulação de frequência (FM).

1. Use uma calculadora gráfica para esboçar um gráfico da e use esse gráfico para dar um esboço, mesmo que grosseiro, do gráfico de .
2. Calcule e, utilizando uma calculadora gráfica, use a expressão de para obter seu gráfico. Compare com o obtido no item (a).

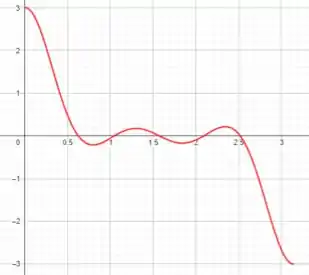
Bom... plotando o gráfico de no intervalo dado, temos:

Analisando o gráfico de , vemos que existem tangentes horizontais (veja aqueles pontos ali em cima).

Isso nos diz então que deve ter zeros na gráfico de .

Então, a partir da simetria do gráfico de devemos ter o gráfico de no ponto mais alto em e no mais baixo em .

Temos na figura os intervalos de crescimento e decrescimento, assim como os sinais de .

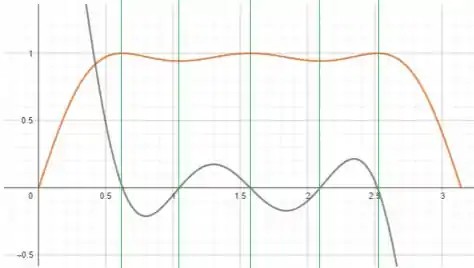
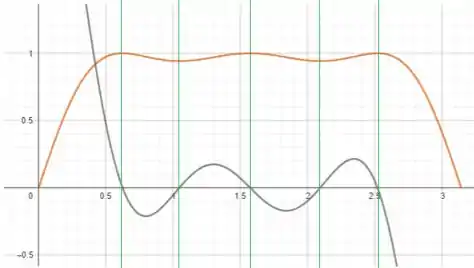
Assim, plotando (em cinza) e mostrando a relação entre os zeros de com os pontos das tangentes de mencionados anteriormente, temos:

Agora vamos derivar :

Aqui vamos usar algumas das regras, como a regra da cadeia, da soma e da função trigonométrica seno.

Da cadeia:

Da soma:

Da função trigonométrica seno:

Vamos devagar então, primeiro com a regra da função trigonométrica e cadeia:

Agora vamos calcular essa nova derivada que surgiu e no fim nós substituímos de volta, aqui vamos usar a regra da soma e outra, a do polinômio:

Vamos lá:

Agora é só substituir de volta, simples assim:

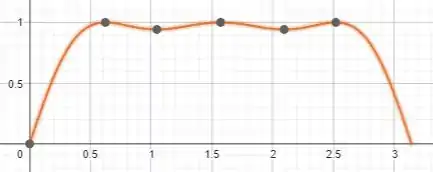
Aqui temos o gráfico de obtido a partir de uma calculadora gráfica:

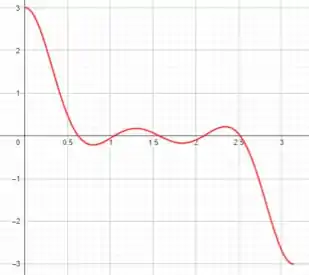
Podemos ver a semelhança entre ele e o do obtido na letra (a).