Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.11 - Ex. 50
Um cabo flexível pendurado sempre tem a forma de uma catenária , em que e são constantes e (veja a Figura e o Exercício ). Faça o gráfico de vários membros da família de funções . Como o gráfico muda quando varia?
Passo 1
Fala aí, tudo belezinha?
Bom essa questão diz pra gente que a catenária
E a expressão que modela o formato de um cabo flexível pendurado, sendo e , constantes e .
E precisaremos fazer o gráfico de vários membros da família de funções
E dizer como o gráfico muda quando varia.
O exercício fala ainda que essa situação está representada na figura 4, do exercício 52.
Primeiramente aqui temos a figura :
Vamos ver o que acontece quando esse varia então.
Passo 2
Podemos fazer isso plotando algumas curvas com diferente valores de e observar o que está acontecendo com o gráfico da nossa função.
Usando uma calculadora gráfica ou um programa para plotar gráficos, podemos observar algo desse tipo aqui.
Aqui temos o gráfico de vários membros da família de funções com :
A partir do gráfico vemos que os pontos que interceptam são iguais a , e vamos que a medida que aumenta, o gráfico vai diminuindo a curvatura.
Resposta
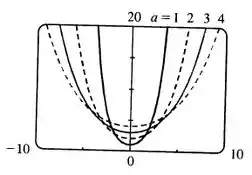
O gráfico vai diminuindo a curvatura a medida que aumenta.