Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 19
Os gráficos se interceptam na janela retangular dada? Se eles se interceptarem, quantos pontos de intersecção existem?
por
Passo 1
Eaee!!! Belezinha? Bom... a questão quer que verifiquemos se as seguintes funções
se interceptam dentro da janela retangular por :
Uma forma de resolver isso é igualando as duas funções para encontrar o ponto de interseção entre elas, e depois verificar se esse ponto está contido na janela.
Então vamos ver se isso acontece.
E aí??? Bora lá? 😉
Passo 2
Vamos começar igualando as duas funções
O que nos dá a equação de segundo grau:
E usando Bhaskara, teremos:
Opa!!! Temos um problema aqui. Nosso Delta deu negativo. Isso indica que nossa equação não possui solução real. Então não teremos ponto de interseção entre os dois gráficos em lugar nenhum.
Muito menos dentro da janela dada. E isso já responde a nossa questão.
Passo 3
Mas pra ela ficar mesmo bem clara e completa, vamos ver isso acontecendo graficamente.
Plotando as funções na janela por , temos:
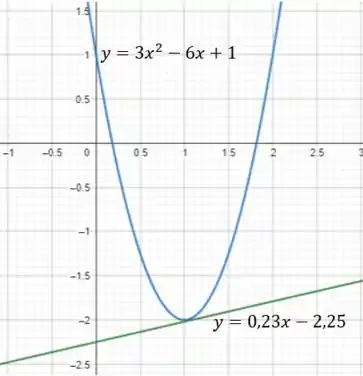
Olhando para essa imagem até parece que a funções se encontram, né? E isso está acontecendo por causa do tamanho da nossa janela.
Mas observe o que acontece se nos aproximarmos mais do suposto ponto de interseção usando uma janela um pouco menor.
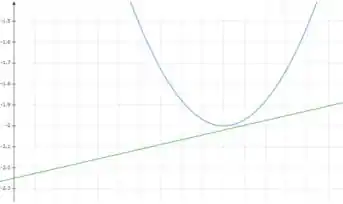
Da pra ver melhor que as curvas estão próximas, porém não se encontram. Então não temos mesmo ponto de interseção nessa janela.
Entendeu direitinho? Responde aee ;)
Resposta
Não temos ponto de interseção nessa janela.