Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 13
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função.
Passo 1
Olá, meu amigo. Vamos juntos resolver mais uma atividade.
Aqui iremos encontrar a janela retangular apropriada para a função dada.
As janelas retangulares são o recorte retangular de um gráfico de uma função exibido por calculadoras e softwares matemáticos. Como temos infinitos valores no plano real, é impossível visualizar o gráfico todo, então é importante escolhermos um intervalo de visualização onde podemos visualizar e entender o corpotamento do gráfico para todos os seus possíveis valores, mas vendo apenas uma janela.
Para determinar uma janela retangular apropriada para o gráfico da função, precisamos considerar alguns aspectos importantes:
1. Comportamento da Função:
- Extensões: É importante identificar os valores máximo e mínimo da função no intervalo de interesse para definir os limites da janela.
- Pontos de interesse: Se a função possui pontos específicos de interesse, como raízes, pontos de inflexão ou assíntotas, a janela deve ser ajustada para capturá-los.
2. Escala e Proporção:
- Visibilidade: A janela deve ser dimensionada de forma que o gráfico da função seja visível e compreensível.
- Proporção: A proporção da janela (largura/altura) deve ser adequada à forma da função para evitar distorções no gráfico.
Uma forma de encontrarmos a janela retangular é analisarmos o domínio e a imagem da função. E a partir daí encontrarmos os valores , , e . Pois o domínio nos dirá informações sobre os possíveis valores de que a função pode assumir e a imagem os possíveis valores de que a função pode assumir. E é isso que iremos fazer aqui.
Passo 2
Considerando a função , sabemos que a função está definida para todos os números reais, de modo que o domínio da função é .
Observando o termo :
Quando traçamos o gráfico da função trigonométrica fornecida, obtemos um período de é um intervalo de em . Pois a função trigonométrica é limitada em :
Multiplicando todos os termos por
Esse será a origem do primeiro limite que teremos em nosso primeiro retângulo de visualização.
Recordando a propriedade de uma função seno, sabemos que o período de é pois o período da função é
e o alcance é como já dito. Assim, o termo tem um valor absoluto maior em comparação com . É um termo dominante.
Observando o termo :
Com base nas propriedades da função trigonométrica mais uma vez, o período de é
e o alcance é considerando que .
No primeiro gráfico onde é dominante, incorporamos o intervalo no intervalo para que possamos incluir o termo . Assim, temos o gráfico por .
Passo 3
Vendo o retângulo :
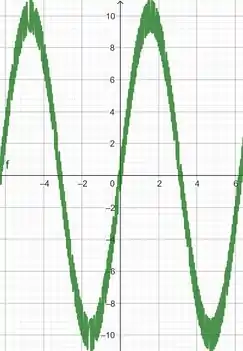
Veja que nosso gráfico está meio ‘ruidoso’, com oscilações menores dentro da continuidade dele. Vamos dar uma aproximada para vermos melhor:
Vamos utilizar o retângulo :
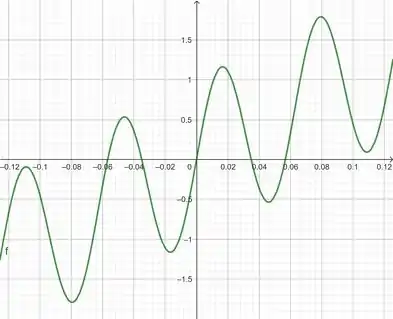
Para mostrar mais detalhes na curva, ampliamos o gráfico anterior. Assim, obtemos o gráfico por .
Resposta
Ver o desenvolvimento.