Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 17.3 - Ex. 7
Uma mola tem massa de presa a ela e sua constante da mola é . A mola é solta em um ponto acima de sua posição de equilíbrio. Faça os gráficos da função posição para os seguintes valores da constante de amortecimento . Que tipo de amortecimento acontece em cada caso?
Passo 1
Olá, tudo bem? A equação diferencial que descreve o movimento de uma massa presa a uma mola é dada pela equação do livro texto:
Essa é uma equação diferencial de segunda ordem, homogênea e de coeficientes constantes. A equação característica associada é:
E a solução é dada pela fórmula de Bháskara:
Aqui podemos ter três tipos de movimento, dependendo do sinal do delta . Vamos analisar casos diferentes.
Passo 2
Primeiro caso, com . Substituindo na solução para temos:
Aqui temos duas raízes complexas do tipo a solução é:
Beleza? Aqui temos e . Vamos substituir os valores encontrados? A solução é:
E as condições de contorno? Temos duas. A primeira nos diz que , então temos:
A segunda condição é sobre a derivada de , então derivando a solução temos:
Aplicando em temos:
Então a solução vai ser:
E o movimento é o subamortecido
Passo 3
Para temos:
Aqui temos duas raízes complexas do tipo a solução é:
Beleza? Aqui temos e . Vamos substituir os valores encontrados? A solução é:
E as condições de contorno? Temos duas. A primeira nos diz que , então temos:
A segunda condição é sobre a derivada de , então derivando a solução temos:
Aplicando em temos:
Então a solução vai ser:
E o movimento continua sendo subamortecido, pois temos raízes complexas.
Passo 4
Para temos:
Aqui temos duas raízes reais e iguais e a solução vai ser do tipo:
E as condições de contorno? Temos duas. A primeira nos diz que , então temos:
A segunda condição é sobre a derivada de , então derivando a solução temos:
Aplicando em temos:
E sabendo que temos:
Então a solução vai ser:
Como temos duas raízes reais iguais, o movimento é classificado como amortecimento crítico.
Passo 5
Para temos:
Aqui temos duas raízes reais e diferentes e a solução vai ser do tipo:
E as condições de contorno? Temos duas. A primeira nos diz que , então temos:
A segunda condição é sobre a derivada de , então derivando a solução temos:
Aplicando em temos:
E sabendo que temos:
E :
Então a solução vai ser:
Aqui temos um movimento superamortecido
Vamos para o último valor de ?
Passo 6
Para temos:
Aqui temos duas raízes reais e diferentes e a solução vai ser do tipo:
E as condições de contorno? Temos duas. A primeira nos diz que , então temos:
A segunda condição é sobre a derivada de , então derivando a solução temos:
Aplicando em temos:
E resolvendo o sistema vamos ter::
E :
Então a solução vai ser:
E também vai ser superamortecido.
O gráfico abaixo mostra todas as soluções juntas:
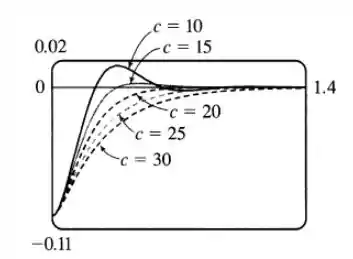
E os movimentos vão ser:
- : subamortecido.
- : subamortecido.
- : amortecimento crítico.
- : superamortecido.
- : superamortecido.
- : subamortecido.
- : subamortecido.
- : amortecimento crítico.
- : superamortecido.
- : superamortecido.
Resposta
Resposta
Ei, a resposta está no passo a passo :)