Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.5 - Ex. 69

Mostre que a elipse x 2 a 2 + y 2 b 2 = 1 e a hipérbole x 2 A 2 - y 2 B 2 = 1 são trajetórias ortogonais se A 2 < a 2 e a 2 - b 2 = A 2 + B 2 (logo, a elipse e a hipérbole possuem os mesmos focos).

Passo 1

Uma vez que A 2 < a 2 , temos a certeza de que existem quatro pontos de interseção:

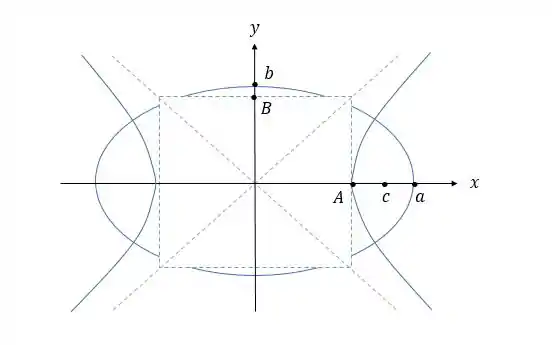
Passo 2

Temos que:

x 2 a 2 + y 2 b 2 = 1

Vamos derivar ambos os lados da equação em relação a x. Ficamos com:

2 x a 2 + 2 y y ' b 2 = 0

Isso implica que:

y y ' b 2 = - x a 2

Isolando y ' , temos que:

y ' = m 1 = - x b 2 y a 2 (1)

Passo 3

Agora, fazendo:

x 2 A 2 - y 2 B 2 = 1

Vamos derivar ambos os lados da equação em relação a x. Ficamos com:

2 x A 2 - 2 y y ' B 2 = 0

Isso implica que:

y y ' B 2 = x A 2

Isolando y ' :

y ' = m 2 = x B 2 y A 2 (2)

Passo 4

Agora, fazendo: m 1 ⋅ m 2 :

m 1 ⋅ m 2 = - x b 2 y a 2 ⋅ x B 2 y A 2 = - b 2 B 2 a 2 A 2 ⋅ x 2 y 2 (3)

Passo 5

E subtraindo as equações 1 - ( 2 ) , temos que:

x 2 a 2 + y 2 b 2 - x 2 A 2 + y 2 B 2 = 0

Isso implica que:

y 2 b 2 + y 2 B 2 = x 2 A 2 - x 2 a 2

⇒ y 2 B 2 + y 2 b 2 b 2 B 2 = x 2 a 2 - x 2 A 2 A 2 a 2

⇒ y 2 b 2 + B 2 b 2 B 2 = x 2 a 2 - A 2 a 2 A 2 (4)

Passo 6

Desde que:

a 2 - b 2 = A 2 + B 2

Nós temos que:

a 2 - A 2 = b 2 + B 2

Então, a equação (4) se torna:

y 2 b 2 B 2 = x 2 A 2 a 2

⇒ x 2 y 2 = A 2 a 2 b 2 B 2

E substituindo na equação (3), temos que:

m 1 ⋅ m 2 = - b 2 B 2 a 2 A 2 ⋅ a 2 A 2 b 2 B 2 = - 1

Portanto, a elipse e a hipérbole são trajetórias ortogonais.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Exercício de Livro
Nos Exercicios de 1 a 28, ache d y d x por derivação implícita5. 1 x + 1 y = 1
Nos Exercicios de 1 a 28, ache d y d x por derivação implícita13. x 3 + x y 3 = 4 y ² ²
Exercício de Livro
Exercício de Livro