Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.5 - Ex. 8
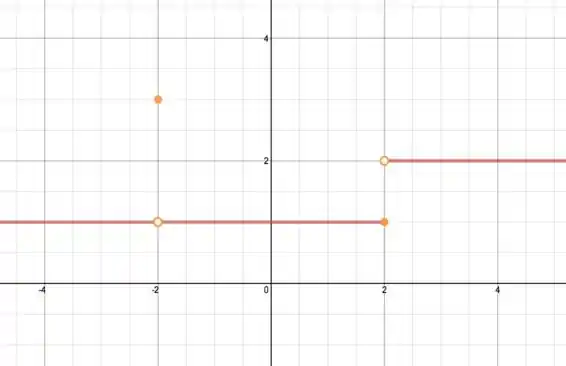
8. Esboce o gráfico de uma função que seja continua exceto para a descontinuidade declarada.
Não é continua à direita nem à esquerda em -2; contínua somente à esquerda em 2
Passo 1
Olá, meu querido colega. Pronto para mais uma resolução?!
Veja bem, aqui a gente quer encontrar uma função que não é continua em apenas um ponto. Que é o que nos foi dito no enunciado. Mas antes de tudo, o que é uma função continua?
Uma função continua tem os seguintes critérios atendidos:
1. está definido.
2. O limite de quando se aproxima de a partir de ambos os lados é igual a . Matematicamente, isso é expresso como:
3. A função está definida para todos os pontos em um intervalo aberto em torno de .
Em outras palavras, não há saltos, lacunas ou quebras abruptas nos gráficos de funções contínuas. Elas podem ter curvas suaves, linhas retas ou até mesmo funções mais complexas, mas a característica essencial é que elas não têm descontinuidades.
Como queremos que nossa função não seja continua nem a esquerda nem a direita do ponto , vamos podemos fazer uma função definida por diversas equações.
Passo 2
Como a função só é continua a esquerda, devemos ter então:
Então ao nos aproximarmos de pela esquerda, deveremos ter o valor da função e do limite iguais. E para podemos ter uma definição única da função para aquele ponto.
Podemos então pensar na seguinte função:
Temos então o gráfico:
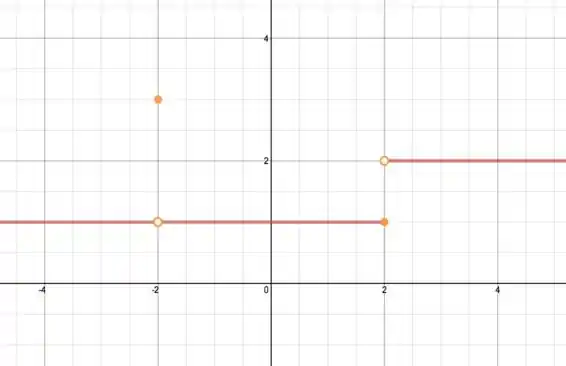
Onde em temos um salto para determinar o valor da função naquele ponto, mas o limite é outro, gerando a descontinuidade pedida. Algo parecido ocorre em mas dessa vez temos a continuidade pedida para
Resposta
