10. a) Mostre que para todo , com , existe um único , com , tal que .
Passo 1
Bem, primeiro, tenha em mente que , significa só podemos ter um dentro desse intervalo aqui:
E como , isso significa basicamente que deve ser diferente de . Ou seja, os valores que realmente nos importa de são esses daqui:
Agora vãos provar isso!
Passo 2
Há de concordar comigo que estará provado que só existe um dentro do intervalo que satisfaz a função, se provar que a função é inteiramente crescente ou decrescente no intervalo, afinal uma função que só cresce ou decresce só pode ser um valor associado a outro, veja o exemplo se duvida disso:
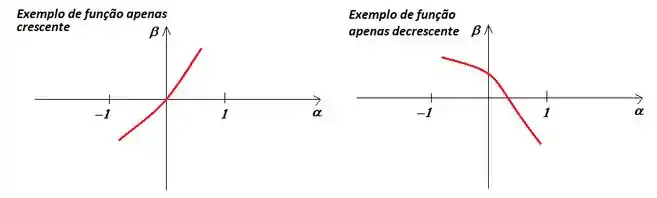
Como a gente pode verificar quanto o crescimento de uma curva? Verificando a derivada da função:
Aplicando a derivada em relação a e tomando cuidado com a regra da fração...
Derivando esses termos...
Ora!!! Para nessas condições desse intervalo aqui:
A derivada é sempre positiva:
O que significa que é sempre crescente com o valor de indo de a . O que significa que só existe de fato um valor de associado a um no intervalo, saca?
Resposta
Questão de demonstração.