Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.4 - Ex. 38
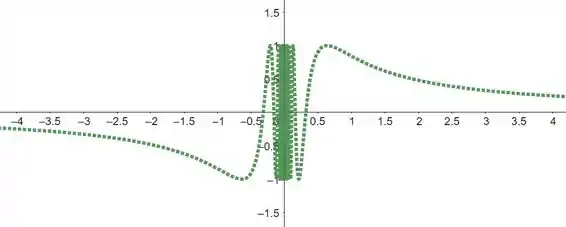
Outra forma de evitar conexões incorretas ao utilizar uma ferramenta gráfica é usar o “modo pontilhado”, o qual desenha apenas os pontos. Se sua ferramenta gráfica permite esse modo, utilize-o para traçar os pontos da função
Passo 1
Esta é uma questão simples que pede apenas o gráfico da função dada. Para isto, precisaremos utilizar recursos tecnológicos para resolvê-la, visto que devemos utilizar linhas pontilhadas ao invés de linhas contínuas ao traçarmos o gráfico da função.
Passo 2
Vejamos então o gráfico da função utilizando linhas pontilhadas abaixo:
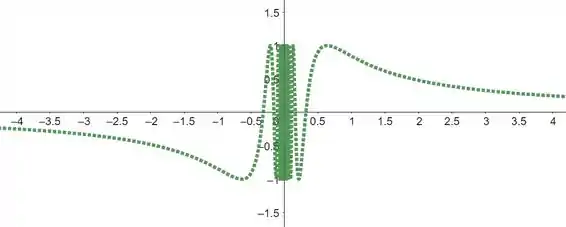
Passo 3
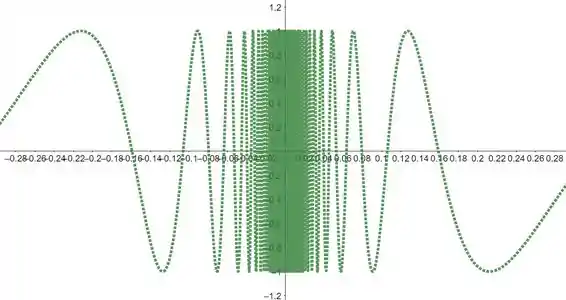
Como pode ser observado no gráfico do passo anterior, temos uma grande oscilação na janela de visualização por , o qual é devido a periodicidade da função seno. Portanto, precisamos dar um “zoom” nesta região. Vejamos abaixo o que ocorre:
A medida em quem diminuímos a nossa janela de visualização, iremos observar mais oscilações da nossa função, passando do ponto máximo até o ponto mínimo. Entretanto, será impossível conseguir detalhar todas as curvas, pois, temos a seguinte relação:
Portanto, o argumento do nosso seno irá para o infinito. Isto implica que ele oscilará infinitamente.
Resposta
