Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 7.1 - Ex. 10
Nos problemas 1-18, use a definição 7.1 para calcular .
10. 
Passo 1
Então galera, para resolvermos os problemas 1-18 temos que lembrar da definição 7.1, assim como o enunciado sugere. Essa definição nos diz o seguinte:
Quando temos apenas uma função definida, obviamente teremos que resolver apenas uma integral, mas quando temos uma função definida a partir de dois ou mais intervalos, teremos que escrever duas ou mais integrais. Prometo que só PARECE complicado, pessoal!
Vamo que vamo por a ideia em prática!
Passo 2
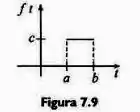
A função que nos foi dada é essa aqui ó:
Aplicando a definição do passo 1, teremos:
E agora o que precisamos fazer é apenas resolver essas integrais, então bora lá!
Passo 3
Resolvendo essas integrais, teremos:
Aplicando o intervalo de integração, teremos:
E está aí nossa Lagrangeana, galeris! 😊