Transformada de Laplace

Fala aí gente bonita, nós somos o Responde Aí. Sejam muito bem vindos.

Nossa missão é dar a você conteúdos didáticos que vão te ajudar a mandar super bem nas suas provas.

Hoje vamos dar uma introduzida em um assunto muito importante, a transformada de laplace.

Transformada de Laplace

A transformada de laplace nada mais é que a transformação de uma função em outra função que chamamos de . Ou seja, a gente pega uma função de e transforma ela em uma função de .

Mas aí você me pergunta: Pra que fazer isso?

A gente usa a transformada de laplace para resolver equações diferenciais ordinárias (EDO), porque quando a gente faz isso a resolução da EDO fica muito muito mais simples. Pra tudo tem um propósito hahaha

Beleza, entendi o porque fazer isso, mas como fazer essa transformação?

Brincadeira, hahahaha.

Nós vamos fazer essa transformação usando essa integral aqui:

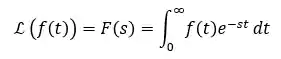
Onde:

• é a função que queremos transformar, e;
• ou é a transformada de laplace da função

Ou seja, se quisermos a transformada de laplace de uma função , devemos realizar essa integral aí de cima.

Bora ver um exemplo para entender melhor como funciona?

Exemplo

Imagina que temos função e queremos calcular a transformada de laplace dela.

Vamos pegar o e substituir lá na nossa integral para o cálculo da transformada de laplace:

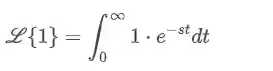
Note que a integral é uma integral imprópria, pois um dos limites é o infinito, então para resolvermos teremos que aplicar o limite, assim:

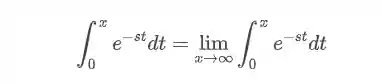
Resolvendo a integral temos:

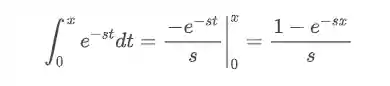
Aplicando o limite, temos:

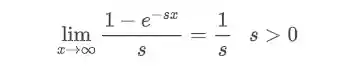
E assim, a transformada de é a seguinte:

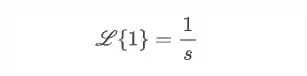
Tranquilo não é?

Mas isso porque a função era , aí a integral fica de boas, mas e se for uma função super complexa? A gente vai ter que sofrer calculando a integral mesmo?

NÃO!!!!

Existe uma tabela onde estão reunidas as transformadas de laplace de diversas funções, inclusive das funções mais conhecidas e que usamos mais como seno, cosseno, , etc. Então, toda vez que precisar calcular a transformada de laplace de uma função basta olhar nessa tabela aqui: Tabela de Transformada de Laplace

Essa foi só a introdução sobre transformada de laplace, ainda tem muita coisa que você precisa aprennder sobre esse assunto. E pensando nisso, nós do Responde Aí, preparamos um Raio-X, onde todo o conteúdo que você precisa está separado em capítulos e tópicos para seu estudo ser bem focado e em ordem lógica.

Está esperando o que para conferir nosso Raio-X aqui embaixo 👇🏽 e ver tudo que o Responde Aí tem para te oferecer?