Nos problemas 51-58, escreva cada função em termos de funções degrau unitário. Encontre a transformada de Laplace da função dada.

Salve salveeee galerinha, bora lá!

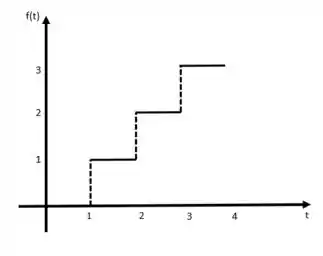
Temos esse gráfico de :

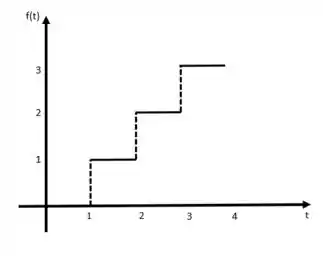
E a primeira coisa que vamos fazer é escrever essa função em termos do degrau unitário. Vamos lá: ela vale para entre 1 e 2, vale para entre 2 e 3 e vale para entre 3 e 4. Então, podemos escrever essa função assim:

Agora vamos calcular a transformada de Laplace disso ok?

Vamos então lembrar algumas transformadas que podemos usar:

E também pode ser útil a propriedade de translação:

Então vamos lá!