Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 7.3 - Ex. 60

Nos problemas 59 e 60, esboce o gráfico da função dada

f t = L - 1 2 s - 3 e - s s 2 + 5 e - 2 s s ²

Passo 1

E aí meu caro!! Bora lá?

Temos essa função:

f t = L - 1 2 s - 3 e - s s 2 + 5 e - 2 s s ²

E queremos esboçar o gráfico dela

Bom, o primeiro passo é encontrar essa transformada inversa de Laplace, certo?

Vamos então lembrar algumas transformadas que podemos usar:

L y t = Y ( s )

L 1 = 1 s

L t n = n ! s n + 1

L e α t = 1 s - α

L c o s ⁡ ( k t ) = s s 2 + k ²

L s e n ⁡ ( k t ) = k s 2 + k ²

L s e n ⁡ ( k t ) = k s 2 + k ²

L f t - a u ( t - a ) = F s . e - a s

E também pode ser útil a propriedade de translação:

L e α . f t = F ( s - α )

Então vamos lá!

Passo 2

Temos

L - 1 2 s - 3 e - s s 2 + 5 e - 2 s s 2

O primeiro termo é a transformada de 2 , e no segundo termo, e no terceiro termo, vamos usar a propriedade:

L f t - a u ( t - a ) = F s . e - a s

Sendo f t = t

Então:

L - 1 2 s - 3 e - s s 2 + 5 e - 2 s s 2 = 2 - 3 t - 1 u t - 1 + 5 t - 2 u ( t - 2 )

Uhuuu encontramos nossa função, agora vamos lá esboçar o gráfico

Passo 3

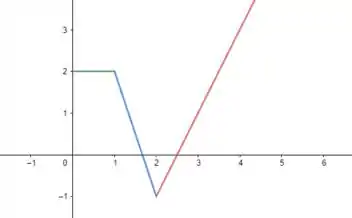
Temos a função

f t = 2 - 3 t - 1 u t - 1 + 5 t - 2 u ( t - 2 )

Essa função vai ser uma constante f t = 2 para 0 < t < 1

Vai valer 2 - 3 t - 1 = - 3 t + 5 para 1 ≤ t < 2

E por fim, vai valer 2 - 3 t - 1 + 5 t - 2 = 2 t - 5 para t ≥ 2

Então:

Boaaa, é isso aí :D

Resposta

Ver Outros Exercícios desse livro