Resolva a equação de Bernoulli dada. Esboce os gráficos das soluções.
Passo 1
Queremos resolver a equação de Bernoulli
Uma equação de Bernoulli é do tipo
Primeiro dividimos a equação por :
Para resolver essa equação, fazemos a substituição
Assim,
Portanto,
Passo 2
Vamos seguir essa raciocínio nesse problema. Note que . Dividindo a equação por :
Ou ainda,
Fazendo a substituição
Assim,
Substituindo na equação:
Portanto,
Passo 3
Essa equação é linear com fator integrante:
Multiplicando a equação por essa fator:
Assim,
Logo,
Para fazer essa integral, usamos partes:
Chamando e , temos que
Logo,
Assim,
Portanto,
Mas como :
Logo,
Ou ainda,
Os gráficos das soluções são:
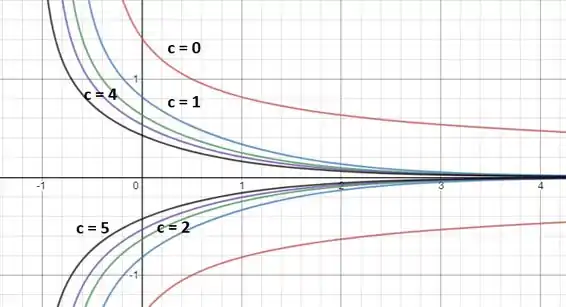
Resposta
Esboço de gráfico.