Resolva
Passo 1
Uma das primeiras formas que encontramos para resolver nossas equações diferenciais é escreve-la na forma de variáveis separáveis
E assim escreve-la da seguinte forma
Daqui é só um passo para resolvemos.
Passo 2
Olhando para nossa equação, já temos que nos considerar com sorte que ela já vem da forma separável. Assim temos que nossa equação pode se reescrita como definimos no passo 1, ou seja
Agora vamos integrar em ambos os lados.
Em ambas as integrais temos que
Então
Assim podemos fazer
Na qual, temos que
Ou seja
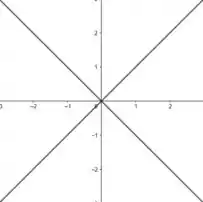
O que nos resulta em um gráfico da seguinte forma com