Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol. 4 - Ed: 5º - Capítulo 12.4 - Ex. 1e

1. Resolva

E)

{[[overset(˙)(x) = - 2 x - 2 y + 3 z],[overset(˙)(y) = - 3 x - y + 3 z],[overset(˙)(z) = - 4 x - 2 y + 5 z]])

Passo 1

Bem, queremos aqui resolver um sistema 3x3. Basicamente a forma de resolução é a mesma dos sistemas 2x2, porém com um cálculo mais chatinho! Mas não se preocupe que vamos destrinchar juntos esses cálculos! Bora?

Primeira coisa é montar a matriz dos coeficientes A baseado no sistema:

A = [[[-,2,-,2,3],[-,3,-,1,3],[-,4,-,2,5]]]

Agora devemos buscar os autovalores dela!

Passo 2

AUTOVALORES:

Os autovalores lambda de uma matriz são do tipo:

det (A - lambda I) = 0

Onde basicamente o que devemos fazer é subtrair lambda na diagonal principal da matriz A , veja:

det ([[-,2,-,lambda,-,2,3],[-,3,-,1,-,lambda,3],[-,4,-,2,5,-,lambda]]) = 0

O determinante de matriz 3x3 é um pouco mais chato que o 2x2. Aqui você tem que repetir as duas primeiras colunas e fazer aquele esquema de multiplicação de diagonais, se lembra?

([[-,2,-,lambda,-,2,3],[-,3,-,1,-,lambda,3],[-,4,-,2,5,-,lambda]]) [[-,2,-,lambda,-,2,],[-,3,-,1,-,lambda,],[-,4,-,2,]] = 0 ->

(- 2 - lambda) (- 1 - lambda) (5 - lambda) + 24 + 18 - 6 (5 - lambda) + 6 (- 2 - lambda) + 12 (- 1 - lambda) = 0

Simplificando isso aí...

(2 + 2 lambda + lambda + lambda^2) (5 - lambda) + 24 + 18 - 30 + 6 lambda - 12 - 6 lambda - 12 - 12 lambda = 0

(10 - 2 lambda + 15 lambda - 3 lambda^2 + 5 lambda^2 - lambda^3) - 12 - 12 lambda = 0

- lambda^3 + 2 lambda^2 + lambda - 2 = 0 ->

lambda^3 - 2 lambda^2 - lambda + 2 = 0

Podemos usar aqui a fatoração por Briot Ruffini para encontrar as raízes dessa equação! Para isso, precisamos de todos os divisores de 2 : +- 1 e +- 2 . Um desses valores deve ser raiz dessa equação. Vejamos se é + 1 :

(+ 1)^3 - 2 (+ 1)^2 - 1 (+ 1) + 2 = 0 ->

1 - 2 - 1 + 2 = 0 -> 0 = 0

Então + 1 é raiz! Substituindo na malha de Briot Ruffini:

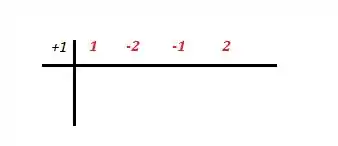
Os números de vermelho são os coeficientes da equação, saca? Aplicando então a técnica:

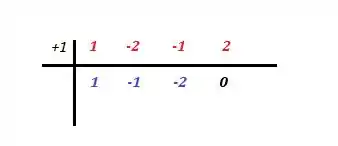
Esses números em azul são os coeficientes de uma equação do segundo grau:

lambda^2 - lambda - 2 = 0 ->

Resolvendo por soma e produto:

lambda_1 = - 1 e lambda_2 = 2

A terceira raiz da equação cúbica foi a primeira que encontramos:

lambda_3 = + 1

O conjunto de soluções fundamentais x^((k)) para cada um deles vão ser:

  • Para o lambda_1 que é real e único...

    • x^((1)) = v_1 e^(lambda_1 t)

  • Para lambda_2 que é real e único...

    • x^((2)) = v_2 e^(lambda_2 t)

  • Para o lambda_3 que é real e único também:

x^((3)) = v_3 e^(lambda_3 t)

Onde v_1 , v_2 e v_3 são os autovetores. Os três autovetores da matriz, como os lambda são todos diferentes, se obtém de forma normal que conhecemos:

(A - lambda_1 I) v_1 = 0

(A - lambda_2 I) v_2 = 0

(A - lambda_3 I) v_3 = 0

Partiu calcular esses autovetores agora?

Passo 3

AUTOVETOR 1:

(A - lambda_1 I) v_1 = 0

Se chamarmos as coordenadas desse vetor v de:

([[a],[b],[c]])

Onde a , b e c são os valores das coordenada dele, se os conhecermos então a gente conhece o autovetor! Substituindo ele no lugar de v :

(A - lambda_1 I) ([[a],[b],[c]]) = 0

Lembre-se de que menos lambda I nada mais é do que subtrair lambda da diagonal principal:

([[-,2,-,lambda_1,-,2,3],[-,3,-,1,-,lambda_1,3],[-,4,-,2,5,-,lambda_1]]) ([[a],[b],[c]]) = 0

Como lambda_1 = - 1 ...

([[-,1,-,2,3],[-,3,0,3],[-,4,-,2,6]]) ([[a],[b],[c]]) = 0

Resolvendo esse produto matricial aí...

{[[- a - 2 b + 3 c = 0],[- 3 a + 3 c = 0],[- 4 a - 2 b + 6 c = 0]])

Das duas primeiras equações, multiplicando a equação de baixo e somando com a de cima, conseguiremos...

a = c

Então...

- c - 2 b + 3 c = 0 ->

- 2 b + 2 c = 0 ->

b = c

Se escolhermos c = 1 , b = 1 e a = 1 ...

v_1 = ([[1],[1],[1]])

Passo 4

AUTOVETOR 2:

(A - lambda_2 I) v_2 = 0

Se chamarmos as coordenadas desse vetor v de:

([[a],[b],[c]])

Novamente teremos...

(A - lambda_2 I) ([[a],[b],[c]]) = 0

Lembre-se de que menos lambda I nada mais é do que subtrair lambda da diagonal principal:

([[-,2,-,lambda_2,-,2,3],[-,3,-,1,-,lambda_2,3],[-,4,-,2,5,-,lambda_2]]) ([[a],[b],[c]]) = 0

Como lambda_2 = 2 ...

([[0,-,2,3],[-,3,-,3,3],[-,4,-,2,3]]) ([[a],[b],[c]]) = 0

Resolvendo esse produto matricial aí...

{[[- 2 b + 3 c = 0],[- 3 a - 3 b + 3 c = 0],[- 4 a - 2 b + 6 c = 0]])

Das duas últimas equações, isolando e substituindo...

b = c ->

- 3 a - 3 c + 3 c = 0 ->

a = 0

Se escolhermos c = 1 , então a = 0 e b = 1 . Logo, o autovetor associado a esse autovalor é:

v_2 = ([[0],[1],[1]])

Passo 5

AUTOVETOR 3:

(A - lambda_3 I) v_3 = v_2

Se chamarmos as coordenadas desse vetor v de:

([[a],[b],[c]])

Novamente teremos...

(A - lambda_3 I) ([[a],[b],[c]]) = 0

Lembre-se de que menos lambda I nada mais é do que subtrair lambda da diagonal principal:

([[-,2,-,lambda_3,-,2,3],[-,3,-,1,-,lambda_3,3],[-,4,-,2,5,-,lambda_3]]) ([[a],[b],[c]]) = 0

Como lambda_3 = 1 ...

([[-,3,-,2,3],[-,3,-,2,3],[-,4,-,2,4]]) ([[a],[b],[c]]) = 0

Resolvendo esse produto matricial aí...

{[[- 3 a - 2 b + 3 c = 0],[- 3 a - 2 b + 3 c = 0],[- 4 a - 2 b + 4 c = 0]])

Das duas últimas equações, multiplicando por - 1 e somando...

- a + c = 0 ->

c = a

Então...

- 3 a - 2 b + 3 a = 0 ->

b = 0

Se escolhermos a = 1 , então c = 1 . Logo, o autovetor associado a esse autovalor é:

v_3 = ([[1],[0],[1]])

Passo 6

Logo, as três soluções fundamentais serão:

x^((1)) = v_1 e^(lambda_1 t)

x^((2)) = v_2 e^(lambda_2 t)

x^((3)) = v_3 e^(lambda_3 t)

Substituindo...

x^((1)) = ([[1],[1],[1]]) e^(- t)

x^((2)) = ([[0],[1],[1]]) e^(2 t)

x^((3)) = ([[1],[0],[1]]) e^t

A solução final é então dada pela expressão:

([[x],[y],[z]]) = c_1 x^((1)) + c_2 x^((2)) + c_3 x^((3)) ->

([[x],[y],[z]]) = c_1 ([[1],[1],[1]]) e^(- t) + c_2 ([[0],[1],[1]]) e^(2 t) + c_3 ([[1],[0],[1]]) e^t

Resposta

([[x],[y],[z]]) = c_1 ([[1],[1],[1]]) e^(- t) + c_2 ([[0],[1],[1]]) e^(2 t) + c_3 ([[1],[0],[1]]) e^t

Ver Outros Exercícios desse livro